如图中,每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≤2)个棋子,每个图案的棋子总数为S,按图的排列规律推断S与n之间的关系可以用式子___________来表示. 
某厂投入200 000元购置生产某新型工艺品的专用设备和模具,共生产这种工艺品 件,又知生产每件工艺品还需投入350元,每件工艺品以销售价550元全部售出,生产这
件,又知生产每件工艺品还需投入350元,每件工艺品以销售价550元全部售出,生产这 件工艺品的销售利润=销售总收入-总投入,则下列说法错误的是( )
件工艺品的销售利润=销售总收入-总投入,则下列说法错误的是( )
A.若产量 ,则销售利润为负值; ,则销售利润为负值; |
B.若产量 ,则销售利润为零; ,则销售利润为零; |
C.若产量 ,则销售利润为 ,则销售利润为 元; 元; |
D.若产量 ,则销售利润随着产量 ,则销售利润随着产量 的增大而增加 的增大而增加 |
某蔬菜店第一次用800元购进某种蔬菜,由于销售状况良好,该店又用1400元第二次购进该品种蔬
菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有3% 的损耗,第二次购进的蔬菜有5% 的损耗,若该蔬菜店售完这些蔬菜获利不低于1244元,则该蔬菜每千克售价至少为多少元?
用 分别表示学校、小明家、小红家,已知学校在小明家的南偏东
分别表示学校、小明家、小红家,已知学校在小明家的南偏东 ,小红家在小明家正东,小红家在学校北偏东
,小红家在小明家正东,小红家在学校北偏东 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
.我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=-(x-60)2+41(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q=-(100-x)2+(100-x)+160(万元).
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法: ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及 ;
; (3)是否存在一点P,使S△PAB=
(3)是否存在一点P,使S△PAB= S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20 时,按2元/
时,按2元/ 计费;月用水量超过20
计费;月用水量超过20 时,其中的20
时,其中的20 仍按2元/
仍按2元/ 收费,超过部分按
收费,超过部分按 元/
元/ 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费 元.
元.
(1)分别求出 和
和 时
时 与
与 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 |
四月份 |
五月份 |
六月份 |
| 交费金额 |
30元 |
34元 |
42.6元 |
小明家这个季度共用水多少立方米?
小明在路灯AB下玩耍时发现自己的影长DF的长是3米,沿着BD方向来到点F处再测得自己的影长FG是4米.如果小明的身高是1.8米,求路灯AB的高度.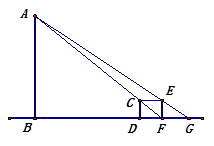
学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
如图,旗杆AB的影子一部分在地面上,另一部分在某一建筑的墙上,小亮测得旗杆AB在地面上的影长BD为9.6 m,在墙面上的影长CD为2 m,同一时刻,小亮又测得竖立于地面1 m长的标杆的影长为1.2 m,请帮助小亮求出旗杆AB的高度.解: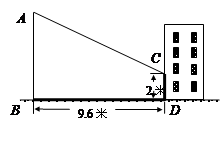
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )
| A.第3天 | B.第4天 | C.第5天 | D.第6天 |

电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,此WORD中为方便大家识别与印刷,我还是把图乙中的0都标出来吧,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)

下面共有四种情景:
A. 一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系);
B. 从树上开始往下掉的苹果(苹果落地前的高度与下落时间的关系);
C. 一杯越来越凉的开水(水温与时间的关系);
D. 竖直向上抛出的篮球(篮球落地前的速度与时间的关系);
上面各种情景可以近似的用下面那个图象来表示(横轴表示时间,纵轴表示相应的因变量),A、B、C、D各情景对应的图象依次为:___________。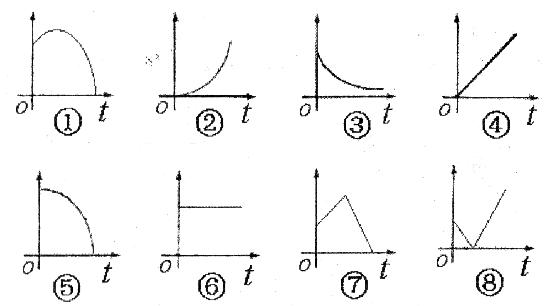
试题篮
()