初中数学应用类问题试题

下列交通标志是轴对称图形的是（　　）

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为．但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道时，我们可以这样做：
观察并猜想：
=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
=（1+0）×1+（1+1）×2+（l+2）×3
=1+0×1+2+1×2+3+2×3
=（1+2+3）+（0×1+1×2+2×3）
=（1+0）×1+（1+1）×2+（l+2）×3+（1+3）×4；
=1+0×1+2+1×2+3+2×3+（ ___________）
=（1+2+3+4）+（___________）
…
归纳结论：
=（1+0）×1+（1+1）×2+（1+2）×3+…[（1+（n-l）]n
=1+0×1+2+1×2+3+2×3+…+n+（n-1）×n
=（___________）+[ ___________]
= （__________）+（ ___________）
=×(___________)
实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是___。

.在一次课题设计活动中，小明对修建一座87m长的水库大坝提出了以下方案；大坝的横截面为等腰梯形，如图，∥，坝高10m，迎水坡面的坡度，老师看后，从力学的角度对此方案提出了建议，小明决定在原方案的基础上，将迎水坡面的坡度进行修改，修改后的迎水坡面的坡度。

（1）      求原方案中此大坝迎水坡的长（结果保留根号）
（2）      如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿方向拓宽2.7m，求坝顶将会沿方向加宽多少米？

一些较大数值问题可以通过用字母代替数成整式问题来解决，请先阅读下面的解题过程，再解答后面的问题．
例： 若x=123456789×123456786，
y=123456788×123456787，
试比较x、y的大小．
解： 设123456788=a，
那么x=， y=
∵
∴x＜y
看完后，你学到了这种方法吗？再亲自试一试吧，你准行！

(1)若x=234567×234568，y=234566×234569，比较比较x、y的大小
(2)计算：

把棱长为4的正方体分割成29个棱长为整数的正方体（且没有剩余），其中棱长为1的正方体的个数为　　．

如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中 所填整数之和都相等，则第2012个格子中的数为（　　）

3

a

b

c

﹣1

2

…

 
A.3     B.2      C.0        D.﹣1

(本小题8分)注意：为了使同学们更好她解答本题，我们提供了—种分析问题的方法，你可以依照这个方法按要求完成本题的解答．也可以选用其他方法，按照解答题的一班要求进行解答即可．
某商品现在的售价为每件35元．每天可卖出50件．市场调查反映：如果调整价格．每降价1元，每天可多卖出2件．请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，最大销售额是多少?设每件商品降价x元．每天的销售额为y元．
(I) 分析：根据问题中的数量关系．用含x的式子填表：

(Ⅱ) (由以上分析，用含x的式子表示y，并求出问题的解)   

如图，一轮船由B处向C处航行，在B处测得C处在B的北偏东75°方向上，在海岛上的观察所A测得B在A的南偏西30°方向上，C在A的南偏东25°方向。若轮船行驶到C处，那么从C处看A，B两处的视角∠ACB是多少度？

把一块直尺与一块三角板如图放置，若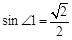，则∠2的度数为（     ）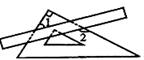

A．120°

B．135°

C．145°

D．150°

如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n的值是

A．48

B．56

C．63

D．74

已知：，，，……
（1）根据你发现的规律写出第（为正整数）个式子是     ；
（2）利用这个规律可得方程
的解是     ．

（本题10分） 
在向红星镇居民介绍王家庄位置的时候，我们可以这样说:如图，在以红星镇为原点，正东方向为x轴正方向，正北方向为y轴正方向的平面直角坐标系（1单位长度表示的实际距离为1km）中，王家庄的坐标为（5，5）；也可以说，王家庄在红星镇东北方向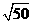km的地方。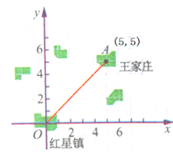
 
还有一种方法广泛应用于航海、航空、气象、军事等领域。如右下图：在红星镇所建的雷达站O的雷达显示屏上，把周角每15°分成一份，正东方向为0°，相邻两圆之间的距离为1个单位长度（1单位长度表示的实际距离为1km），现发现2个目标，我们约定用（10，15°）表示点M在雷达显示器上的坐标，则：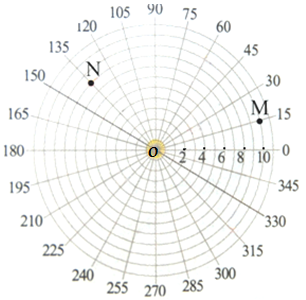

（1）点N可表示为          ；王家庄位置可表示为          ；点N关于雷达站点0成中心对称的点P的坐标为         ；
（2）S△OMP=                 ；
（3）若有一家大型超市A在图中（4，30°）的地方，请直接标出点A，并将超市A与雷达站O连接，现准备在雷达站周围建立便民服务店B，使得△ABO为底角30°的等腰三角形，请直接写出B点在雷达显示屏上的坐标.

小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（ 　）

A．矩形

B．正方形

C．等腰梯形

D．无法确定

甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为40km．他们前进的路程为s(km)，甲出发后的时间为t(h)，甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法不正确的是（ ▲ )

A．甲的速度是10km/h            B．乙的速度是20km/h
C．乙出发h后与甲相遇         D．甲比乙晚到B地2h

据统计，2010年中国粮食总产量达到546 400 000吨，用科学记数法表示为（ ▲ )

A．5.464×10^7吨

B．5.464×10^8吨

C．5.464×10^9吨

D．5.464×10^10吨