初中数学应用类问题试题

爱动脑筋的小明制造了一个小黑匣，只要你输入一个数字，它就输出另一个数来，好奇心强的小亮赶紧试试了一下，结果得到了下面的表格

输入	2	5	10	17	26	37	…
输出	1						…

聪明的你一定知道当输入的数是65时，输出的结果是       

如图所示，是我们常用的一副三角板．请你用一副三角板画出度数分别为15°和135°的两个角．（要求：保留画图痕迹）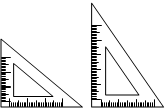

（2）
在下面的方格纸中经过点C画与线段AB互相平行 的直线l1，再经过点B画一条与线段AB垂直的直线l2．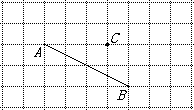

某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1．在温室内，沿前侧内墙保留3m宽的空地，其它三侧内墙各保留1m宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是288m²？

我国从2008年6月1日起执行“限塑令”．“限塑令”执行前，某校为了了解本校学生所在家庭使用塑料袋的数量情况，随机调查了10名学生所在家庭月使用塑料袋的数量，结果如下（单位：只）：
65，70，85，75，85，79，74，91，81，95．
（1）计算这10名学生所在家庭平均月使用塑料袋多少只？
（2）“限塑令”执行后，家庭月使用塑料袋数量预计将减少50%．根据上面的计算结果，估计该校1 000名学生所在家庭月使用塑料袋可减少多少只？

某渔场计划购买甲、乙两种鱼苗共6000尾，甲种鱼苗每尾0.5元，乙种鱼苗每尾0.8元．相关资料表明：甲、乙两种鱼苗的成活率分别为90%和95%．
（1）若购买这批鱼苗共用了3600元，求甲、乙两种鱼苗各购买了多少尾？
（2）若购买这批鱼苗的钱不超过4200元，应如何选购鱼苗？
（3）若要使这批鱼苗的成活率不低于93%，且购买鱼苗的总费用最低，应如何选购鱼苗？

观察下列图形（每幅图中最小的三角形都是全等的），请写出第个图中最小的三角形的个数有          个．

（本题8分）如图，在梯形ABCD中，AD//BC，E是AD的中点，BC=5，AD=12，梯形高为4，∠A =45°，P为AD边上的动点.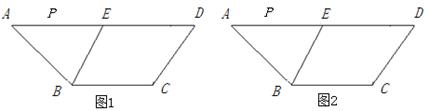

（1）当PA的值为____________时，以点P、B、C、E为顶点的四边形为直角梯形；
（2）当PA的值为____________时，以点P、B、C、E为顶点的四边形为平行四边形；
（3）点P在AD边上运动的过程中，以P、B、C、E为顶点的四边形能否构成菱形？如果能，求出PA长．如果不能，也请说明理由.

如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t，正方形除去圆部分的面积为S（阴影部分），则S与t的大致图象为（   ）

第12题

如图所示，河堤横断面迎水坡AB的坡比是1：，堤高BC=5m，则坡面AB的长度是（     ）

A．10m

B．10m

C．15m

D．5m

（本题6分）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造如下正方形：

再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、

序号	①	②	③	④	…
周长	6	10			…

③、④、 …相应长方形的周长如下表所示：
仔细观察图形，上表中的            ，           .
若按此规律继续作长方形，则序号为⑧的长方形周长是              。

为了防控甲型H1N1流感，某校积极进行校园环境消毒，购买了甲、乙两种消毒液共100瓶，其中甲种6元/瓶，乙种9元/瓶．
（1）如果购买这两种消毒液共用780元，求甲、乙两种消毒液各购买多少瓶？
（2）该校准备再次购买这两种消毒液（不包括已购买的100瓶），使乙种瓶数是甲种瓶数的2倍，且所需费用不多于1200元（不包括780元），求甲种消毒液最多能再购买多少瓶？

（本题8分）如图，四边形ABCD是矩形,点O在矩形上方，点B绕着点O逆时针旋转后的对应点为点C．

（1）画出点A绕着点O逆时针旋转后的对应点E；
（2）连接CE,证明：CO平分∠ECD
（3）在（1）（2）的条件下，连接ED,猜想ED与CO的位置关系，并证明你的结论.

2012年3月5日上午9时，十一届全国人大五次会议在人民大会堂开幕。温家宝总理在全国人大会议的政府工作报告中指出，2012年国家财政性教育经费支出21984.63亿元，占国内生产总值4%以上。中央预算内投资用于教育的比重达到7%左右。将21984.63用四舍五入法取近数（精确到0.1）表示应为（   ）

A．21985

B．21984.6

C．21980

D．21900

（本题6分）某市民广场地面铺设地砖，决定采用黑白2种地砖，按如下方案铺设，首先在广场中央铺2块黑色砖（如图①），然后在黑色砖的四周铺上白色砖（如图②），再在白色砖的四周铺上黑色砖（如图③，再在黑色砖的四周铺上白色砖（如图④）这样反复更换地砖的颜色，按照这种规律，直至铺满整个广场．观察下图，解决下列问题．

⑴ 填表

图形序号数	①	②	③	④	…
地砖总数（包括黑白地砖）	2

⑵ 按照这种规律第个图形一共用去地砖多少块?（用含的代数式表示）

2010年春季我国西南五省持续干旱，旱情牵动着全国人民的心。“一方有难、八方支援”，某厂计划生产1800吨纯净水支援灾区人民，为尽快把纯净水发往灾区，工人把每天的工作效率提高到原计划的1.5倍，结果比原计划提前3天完成了生产任务．求原计划每天生产多少吨纯净水？