初中数学圆幂定理试题

绍兴是著名的桥乡，如图，圆拱桥的拱顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（    ）

A．4m

B．5m

C．6m

D．8m

如图，C是⊙O上一点，O是圆心．若∠AOB=80°，则∠ACB的度数为（ ）

A．80°

B．100°

C．160°

D．40°

⊙A半径为5，圆心A的坐标为（1，0），点P的坐标为（-2，4），则点P与⊙A的位置关系是（    ）

A．点P在⊙A上	B．点P在⊙A内
C．点P在⊙A外	D．点P在⊙A上或外

如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．

（1）求证：直线BD与⊙O相切；
（2）若AD：AE＝4：5，BC＝6，求⊙O的直径．

如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．

已知AB为⊙O的直径AC、AD为⊙O的弦，若AB=2AC=AD，则∠DBC的度数为________．

如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（    ）

A．2        B．2        C．2        D．8

如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为   

如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC

（1）若∠CBD=39°，求∠BAD的度数
（2）求证：∠1=∠2

如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．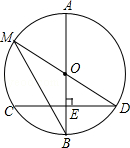

（1）若CD＝16，BE＝4，求⊙O的半径；
（2）若∠M＝∠D，求∠D的度数．

如图，AB是⊙O的直径，弦BC长为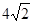，弦AC长为2，∠ACB的平分线交⊙O于点D，求AB和AD的长．

如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，点B是⊙O上一点，连接BP并延长，交直线l于点C，使得AB=AC．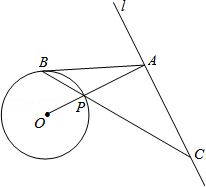

（1）求证：AB是⊙O的切线；
（2）若PC=2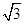，OA=3，求⊙O的半径．

如图，半圆O的直径AB长度为6，半径OC⊥AB，沿OC将半圆剪开得到两个圆心角为90°的扇形．将右侧扇形向左平移，使得点A与点O′，点O与点B分别重合，则所得图形中重叠部分的面积为______．

如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D。

（1）求证：BC是⊙O切线；
（2）若BD=5， DC=3，求AC的长。

已知：如图，C，D是以AB为直径的⊙O上的两点，且OD∥BC．求证：AD=DC。