初中数学圆幂定理选择题

如图，点C、D是以线段AB为公共弦的两条圆弧的中点，AB=4，点E、F分别是线段CD，AB上的动点，设AF=x，AE²－FE²=y，则能表示y与x的函数关系的图象是（  ）

如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（ ）

A．2     B．8      C．2       D．2

如图，在⊙O中，∠ABC=130°，则∠AOC等于（  ）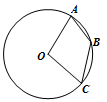
 

A．50°

B．80°

C．90°

D．100°

如图，矩形ABCD为⊙O的内接四边形，AB=2，BC=3，点E为BC上一点，且BE=1，延长AE交⊙O于点F，则线段AF的长为（  ）

A．

B．5

C．＋1

D．

如图，点A、B、C都在⊙O上，⊙O的半径为2，∠ACB＝30°，则弧AB的长是

A．          B．             C．         D．

如图，△ABC是⊙O的内接三角形，∠OAB=35°，则∠ACB的度数为（   ）

A．35°

B．55°

C．60°

D．70°

如图，AB、CD都是⊙O的弦，且AB⊥CD，若∠CDB=62°，则∠ACD的大小为（   ）

A．28°    B．31°    C．38°    D．62°

如下图，当宽为3 cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm），那么该圆的半径为(    )

A．

B．

C．5

D．4

如图，AB是⊙O的直径，C，D是⊙O上的两点，若∠ABC＝70°，则∠BDC的度数为（   ）

A．40°

B．30°

C．20°

D．10°

如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是（  ）

A．35 °

B．45°

C．55°

D．65°

如图， $AC$是 $\odot O$的切线，切点为 $C$， $BC$是 $\odot O$的直径， $AB$交 $\odot O$与点 $D$，连接 $OD$，若 $\angle BAC=55°$，则 $\angle COD$的大小为（     ）

A．

70°

B．

60°

C．

55°

D．

35°

一个圆锥的底面半径为8cm，其侧面展开图的圆心角为240°，则此圆锥的侧面积为（   ）

A．

B．

C．

D．

已知⊙O的直径是16cm，点O到同一平面内直线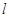的距离为9cm，则直线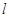与⊙O的位置关系是（ ）

A．相交

B．相切

C．相离

D．无法判断

如图，点A、B、C是⊙O上三点，∠AOC=120°，则∠ABC等于（ ）

A．50°    B．60°    C．65°    D．70°

如图，用直角三角板经过两次画图找到圆形工件的圆心，这种方法应用的道理是（   ）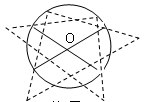

A．垂径定理

B．勾股定理

C．直径所对的圆周角是直角

D．90^0的圆周角所对的弦是直径