初中数学圆幂定理试题

如图，在平面直角坐标系中，已知点E和F的坐标分别为E（0，-2）、F（，0），P在直线EF上，过点P作⊙O的两条切线，切点分别为A、B，使得∠APB=60°，若符合条件的点P有且只有一个，则⊙O的半径为        ．

如图，已知Rt△ABC是⊙O的内接三角形，其中直角边AC=6、BC=8，则⊙O的半径是_________．

如图，在⊙O中，AB是直径， CD是弦，AB⊥CD。

（1）P是优弧CAD上一点（不与C、D重合），求证：∠CPD=∠COB；
（2）点P在劣弧CD上（不与C、D重合）时，∠CPD与∠COB数量关系是什么？（直接写出答案）

如图，AB为半圆O的在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③，④OD：OC=DE：EC，⑤，正确的有（ ）

A．2个      B．3个      C．4个      D．5个

已知，如图，是以线段为直径的的切线，交于点，过点作弦垂足为点，连接
（1）仔细观察图形并写出四个不同的正确结论：
①________，②________ ，③________，④____________
（不添加其它字母和辅助线，不必证明）；
（2）=，=，求的半径

如图，AB是⊙O的直径，M是⊙O上的一点，MN⊥AB，垂足为N，P，Q分别为弧AM、弧BM上一点（不与端点重合）如果∠MNP=∠MNQ，给出下列结论：
①∠1=∠2；②∠P+∠Q=180°；③∠Q=∠PMN；④MN²=PN•QN；⑤PM=QM
其中结论正确的序号是（ ）

A．①②③

B．①③④

C．①③⑤

D．④⑤

已知，如图：AB为⊙O的直径，AB＝AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC＝45°。给出以下五个结论：

①∠EBC＝22．5°；
②BD＝DC；
③AE＝2EC；
④劣弧是劣弧的2倍；
⑤DE＝DC。
其中正确结论有________．

圆心角为60°，半径为4cm的扇形的弧长为      cm．

如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③DC平分∠ADE；④CG²=AG×BG其中结论正确的是（   ）

A．①②     B．①②③     C．①②④      D．①②③④

如图，⊙O是△ABC的外接圆，∠B=60⁰，0P⊥AC于点P，OP=2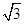，则⊙O的半径为【   】．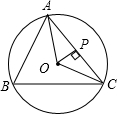

A．4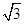

B．6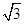

C．8

D．12

 已知半径为1cm的圆，在下面三个图中AC=10cm，AB=6cm，BC=8cm，在图2中∠ABC=90°．

（1）如图1，若将圆心由点A沿AC方向运动到点C，求圆扫过的区域面积；
（2）如图2，若将圆心由点A沿ABC方向运动到点C，求圆扫过的区域面积；
（3）如图3，若将圆心由点A沿ABCA方向运动回到点A．
则I）阴影部分面积为_   ___；Ⅱ）圆扫过的区域面积为__   __．

已知等边△ABC和⊙M.
（1）如图l，若⊙M与BA的延长线AK及边AC均相切，求证： AM∥BC;
（2）如图2，若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切，求证：四边形ABCM是平行四边形．

如图△ABC中，BC=3，以BC为直径的⊙O交AC于点D，若D是AC中点，∠ABC=120°.
（1）求∠ACB的大小；
（2）求点A到直线BC的距离．

如图，圆弧形桥拱的跨度AB＝16米，拱高CD＝4米，则拱桥的半径为    。

如图，△ABC中，∠C＝90°，⊙O分别切AB、BC、AC于D、E、 F，若AD＝5cm，BD＝3cm，试求出△ABC的面积。