初中数学立体图形解答题

要制造一个长方体箱子，底面为正方形，体积为，且长方体的高是底面边长的2倍。
（1）求长方体的底面边长；
（2）求长方体的表面积。

如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．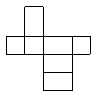

（1）请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；
（2）若图中的正方形边长为2cm，长方形的长为3cm，宽为2cm，请直接写出修正后所折叠而成的长方体的体积：          cm³．

（1）解方程：=
（2）小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分)，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子． 注意：只需添加一个符合要求的正方形，并用阴影表示．

回答下列问题：
（1）如图所示的甲、乙两个平面图形能折成什么几何体？_________________________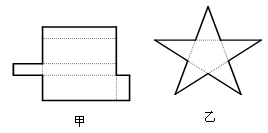

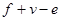（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为，顶点个数为，棱数为，分别计算第（1）题中两个多面体的的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．

图(1)是正方体木块，把它切去一块，可能得到形如图(2)、(3)、(4)、(5)的木块。

我们知道，图(1)的正方体木块有8个顶点，12条棱，6个面，请你将图(2)，(3)，(4)，(5)中木块的顶点数，棱数，面数填入下表：

图	顶点数	棱数	面数
(1)	8	12	6
(2)
(3)
(4)
(5)

 
观察上表，请你归纳上述各种木块的顶点数，棱数，面数之间的数量关系，这种数量关系是：_______________

将长为1，宽为a的长方形纸片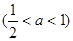如图左那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图右那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．
（1）第一次操作后，剩下的长方形的长和宽分别为多少？（用含a的代数式表示）
（2）第二次操作后，剩下的长方形的面积是多少？（列出代数式，不需化简）
（3）假如第二次操作后，剩下的长方形恰好是正方形，则a的值是多少？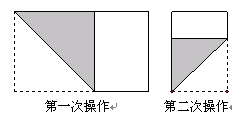

由5个相同的小立方块搭成的几何体如图所示，请把网格中的三视图画完整．

一个正方体的六个面上分别标有1、2、3、4、5、6，根据图中从各个方向看到的数字，解答下面的问题：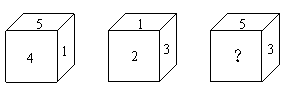

（1）“？”处的数字是什么？
（2）每两个相对面上的数字分别是什么？

连线题
把图中第一行的展开图与第二行中相对应的几何体用线连接起来．

现将一个长为4厘米，宽为3厘米的长方形，分别绕它的长、宽所在的直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？

假如圆锥的体积一定，它的底面直径与高（   ）

A．成正比例

B．成反比例

C．不成比例

D．无法确定

书籍是人类进步的阶梯！为爱护书一般都将书本用封皮包好．
问题1：现有精装词典长、宽、厚尺寸如图（1）所示（单位：cm），若按图（2）的包书方式，将封面和封底各折进去3cm．试用含a、b、c的代数式分别表示词典封皮（包书纸）的长是      cm，宽是       cm；
问题2：在如图（4）的矩形包书纸皮示意图中，虚线为折痕，阴影是裁剪掉的部分，四角均为大小相同的正方形，正方形的边长即为折叠进去的宽度．
（1）若有一数学课本长为26cm、宽为18.5cm、厚为1cm，小海宝用一张面积为1260cm2的矩形纸包好了这本数学书，封皮展开后如图（4）所示．若设正方形的边长（即折叠的宽度）为x cm，则包书纸长为       cm，宽为        cm（用含x的代数式表示）．
（2）请帮小海宝列好方程，求出第（1）题中小正方形的边长x cm．

如图,四种图形各是哪种立体图形的表面展开所形成的?画出相应的四种立体图形.

下图是由五块积木搭成，这几块积木都是相同的正方体，请画出这个图形的主视图、左视图和俯视图。

如图是由7块小正方体组成的立体图形，画出它的主视图、俯视图、左视图．