如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
| A.甲正确,乙错误 | B.乙正确,甲错误 |
| C.甲、乙均正确 | D.甲、乙均错误 |
将边长分别为1、1、2、3、5的正方形依次选取2个、3个、4个、5个拼成,按下面的规律依次记作①、②、③、④.若继续选取适当的正方形拼成,那么按此规律,⑧的周长应该为( )
| A.288 | B.220 | C.178 | D.110 |
如图,A( ,1),B(1,
,1),B(1, ),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
A.(- ,1) ,1) |
B.(-2,0) |
C.(-1,- )或(-2,0) )或(-2,0) |
D.(- ,-1)或(-2,0) ,-1)或(-2,0) |
若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是
称为x的差倒数,如2的差倒数是 =-1,-1的差倒数为
=-1,-1的差倒数为 .现已知
.现已知 ,
, 是
是 的差倒数,
的差倒数, 是
是 的差倒数,
的差倒数, 是
是 的差倒数,…,依次类推,则
的差倒数,…,依次类推,则 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D.4 |
有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6),以小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线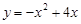 上的概率为( )
上的概率为( )
A.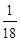 B.
B.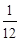 C.
C.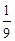 D.
D.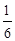
如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为()
A.22 B.20 C.18 D.16
如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为()。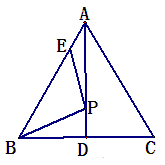
A.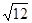 |
B.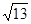 |
C.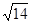 |
D.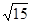 |
如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合),以BD、BF为邻边作平行四边形BDEF,又AP綊BE(点P、E在直线AB的同侧),如果BD= AB,那么△PBC的面积与△ABC的面积之比为( )
AB,那么△PBC的面积与△ABC的面积之比为( )
A. B.
B. C.
C. D.
D.
如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动,设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )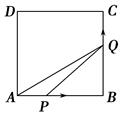
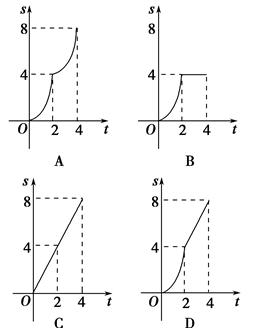
如右图是一个高为10cm的圆柱形烧杯,内有一个倒立的化学滤纸做的圆锥,圆锥的高与圆柱的高相等,圆锥的底面积与圆柱的底面积相等。在小学我们学过:这时圆柱的体积是圆锥的体积的3倍。现在向滤纸中倒入一些溶液,记滤纸内的溶液体积为V1,烧杯内的溶液(含滤纸中的溶液)体积为V2,设烧杯中溶液的高度为h cm,y=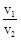 ;则y与h的函数图像大致是
;则y与h的函数图像大致是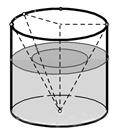
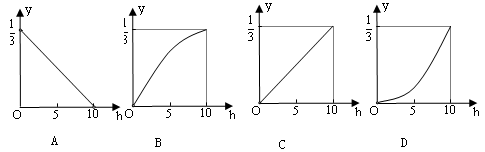
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为
A. 2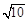 B. 2
B. 2 C. 2
C. 2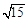 D. 8
D. 8
试题篮
()