如图,AB切⊙O于点B,OA=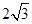 ,∠A=30°,弦BC∥OA,则劣弧
,∠A=30°,弦BC∥OA,则劣弧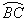 的弧长为
的弧长为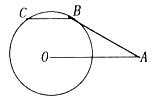
A.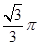 |
B. |
C.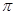 |
D.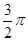 |
在半径为1的⊙O中,弦AB的长为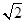 ,则弦AB所对的圆周角的度数为
,则弦AB所对的圆周角的度数为
| A.45° | B.60° | C.45°或135° | D.60°或120° |
如图,四个正六边形的面积都是6,则图中△ABC的面积等于( ).
| A.12 | B.13 | C.14 | D.15 |
如图:点P(x,y)为平面直角坐标系内一点,PB⊥x 轴,垂足为B, A为(0,2),若PA=PB,则以下结论正确的是( ).
A.点P在直线 上 上 |
B.点P在抛物线 上 上 |
C.点P在抛物线 上 上 |
D.点P在抛物线 上 上 |
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的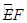 上时,
上时, 的长度等于( ).
的长度等于( ).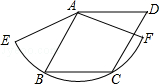
A.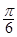 B.
B.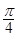 C.
C.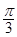 D.
D.
如图,函数y=-kx(k 与
与 的图象交于A、B两点,过A作AC
的图象交于A、B两点,过A作AC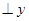 轴于C,则
轴于C,则 BOC的面积是( ).
BOC的面积是( ).
A.8 B .4C. 2 D.1
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则下列图象中,能表示y与x的函数关系的图象大致是( )

如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知该图案的面积为 ,小正方形的面积为4,若用
,小正方形的面积为4,若用 表示小矩形的两边长,请观察图案,指出以下关系式中不正确的是( )
表示小矩形的两边长,请观察图案,指出以下关系式中不正确的是( )
A. |
B. |
C. |
D. |
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为

.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为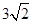 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是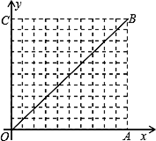
| A.13 | B.14 | C.15 | D.16 |
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为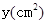 ,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是()
,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是()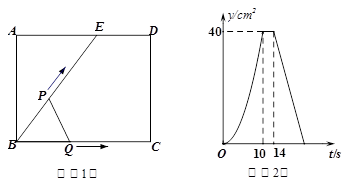
| A.AE=8 |
B.当0≤t≤10时,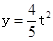 |
C.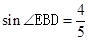 |
D.当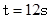 时,△BPQ是等腰三角形 时,△BPQ是等腰三角形 |
如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是
A. B.
B. C.
C. D.
D.
如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A。C分别在x轴、y轴上,反比例函数 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN。
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN。
下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为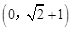 。
。
其中正确的个数是【】
A.1 B.2 C.3 D.4
如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是【】
| A.AE=6cm | B. |
C.当0<t≤10时, |
D.当t=12s时,△PBQ是等腰三角形 |
试题篮
()