如图,抛物线 与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
与x轴交于点A、B两点,与y轴交于点C,且A点坐标(-3,0),连接BC、AC.
(1)求该抛物线解析式;
(2)求AB和OC的长;
(3)点E从点B出发,沿x轴向点A运动(点E与点A、B不重合),过点E作直线l平行AC,交BC于点D,设BE的长为m,△BDE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(4)在(3)的条件下,连接CE,求△CDE面积的最大值.
如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.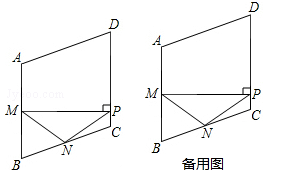
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
(1)求证:直线AE是⊙O的切线;
(2)若∠D=60°,AB=6时,求劣弧 的长(结果保留π).
的长(结果保留π).
已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数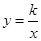 (
(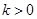 )的图象经过点D且与边BA交于点E,连接DE.
)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为2,则k=;
(2)连接CA,DE与CA是否平行?请说明理由;
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:
(1)填空:乙的速度是米/分;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
请将下列证明过程补充完整:
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.
证明:因为∠1=∠2(已知),
又因为∠1=∠ANC(),
所以(等量代换).
所以∥(同位角相等,两直线平行),
所以∠ABD=∠C().
又因为∠A=∠F(已知),
所以∥().
所以(两直线平行,内错角相等).
所以∠C=∠D().
试题篮
()