在平面直角坐标系中,点A、B、C的坐标分别为(2,0),(3, ),(1,
),(1, ),点D、E的坐标分别为(m,
),点D、E的坐标分别为(m, m),(n,
m),(n, n)(m、n为非负数),则CE+DE+DB的最小值是.
n)(m、n为非负数),则CE+DE+DB的最小值是.
如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长.
如图,在平面直角坐标系中直线 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线 向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是.
向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是.
在直角三角形ABC中, ,
, 是斜边AB的中点,过
是斜边AB的中点,过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点 ,
, …,
…, ,分别记
,分别记 ,
, ,
, ,…,
,…, 的面积为
的面积为 ,
, ,
, ,…
,… ,则
,则 .
.
如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是.
的图象经过点C,交AB于点D,则点D的坐标是.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上, OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当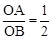 时,
时, 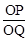 的值为;当
的值为;当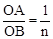 时,
时,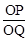 为.(用含n的式子表示)
为.(用含n的式子表示)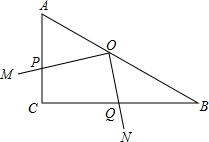
如图,P是抛物线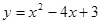 上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=2相切时,点P的坐标为.
上的一点,以点P为圆心、1个单位长度为半径作⊙P,当⊙P与直线y=2相切时,点P的坐标为.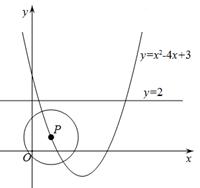
如图,在平面直角坐标系中,ΔABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数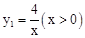 的图象上.反比例函数
的图象上.反比例函数 的图象经过点C,交AB于点D,则点D的坐标是.
的图象经过点C,交AB于点D,则点D的坐标是.
如图,等边△ABC在直角坐标系xOy中,已知 ,
, ,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,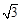 cm为半径的圆与△
cm为半径的圆与△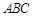 的边相切,请写出t可取的所有值.
的边相切,请写出t可取的所有值.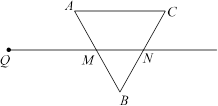
如图,直径分别为CD.CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=10,设弧CD.弧CE的长分别为 .
. ,线段ED的长为
,线段ED的长为 ,则
,则 的值为.
的值为.
如图,在△ABC中,∠ACB=90º,∠B=30º,AC=1,AC在直线l上.将△ABC在直线l上顺时针滚动一周,滚动过程中,三个顶点B,C,A依次落在P1,P2,P3处,此时AP3= ;按此规律继续旋转,直到得点P2012,则AP2012= .
如图,Rt△ABC中,O为坐标原点,∠AOB=90°,∠B=30°,如果点A在反比例函数 (x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
(x>0)的图象上运动,那么点B在函数(填函数解析式)的图象上运动.
如图,在Rt△AOB中,OA=OB=3 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为.
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为.
试题篮
()