如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点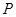 落在反比例函数
落在反比例函数 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在 轴上,一个顶点落在
轴上,一个顶点落在 轴上.
轴上.
(1)图1中的每一个小正方形的面积是;
(2)按照图1 图2
图2 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第 个图形中每一个小正方形的面积是.(用含
个图形中每一个小正方形的面积是.(用含 的代数式表示)
的代数式表示)
如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .
如图,平面直角坐标系的长度单位是厘米,直线 分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t=秒.
分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t=秒.
如图,点P是反比例函数
图象上的点,PA垂直x轴于点A
,点
的坐标为
,
交y轴于点
,连结
,已知
。
(1)k的值是
;
(2)若
是该反比例函数图象上的点,且满足
,则a的取值范围是。
如图,A,B,C为⊙O上相邻的三个n等分点, ,点E在
,点E在 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p=.
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p=.
(参考数据: ,)
,)
如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OBA的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是 .
如图,平面直角坐标系中,已知直线 上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转900至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线
上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转900至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线 交于点A,且BD=2AD,连接CD,直线CD与直线
交于点A,且BD=2AD,连接CD,直线CD与直线 交于点Q,则点Q的坐标为。
交于点Q,则点Q的坐标为。
在平面直角坐标系中,作△OAB,其中三个顶点分别为O(0,0),B(1,1)A(x,y)( 均为整数),则所作△OAB为直角三角形的概率是。
均为整数),则所作△OAB为直角三角形的概率是。
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为 .
今年,6月12日为端午节。在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况。请根据小丽提供的信息,解答小华和小明提出的问题。
(1)小华的问题解答: ;
(2)小明的问题解答: 。
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 (结果保留根号).
正方形ABCD中,AC、BD相交于点O,点E是射线AB上一点,点F是直线AD上一点,BE=DF,连接EF交线段BD于点G,交AO于点H.若AB=3,AG= ,则线段EH的长为 .
,则线段EH的长为 .
已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .
两个反比例函数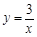 ,
, 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点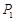 ,
, ,
,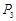 ,…,
,…,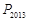 在函数
在函数 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是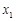 ,
, ,
, ,…,
,…,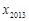 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点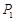 ,
, ,
,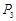 ,…,
,…,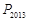 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数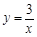 的图像交点依次是
的图像交点依次是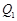 (
(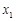 ,
,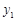 ),
),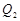 (
( ,
,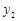 ),
),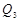 (
( ,
,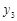 ),…,
),…, (
(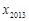 ,
,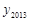 ),则
),则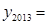 .
.
试题篮
()