初中物理力和机械综合题

如图甲是一台落地电风扇，电风扇的参数见下表；乙图是电风扇的尺寸示意图，由于电风扇的质量分布不均匀，它的重力作用点在P点；电风扇内部的电路图可简化为丙图，图中的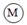代表电动机，R₁、R₂是限流电阻。

（1）小明想在电路中加一个“倾倒开关”，使电风扇被碰倾倒时能自动断开电路。此开关应该安装在丙图中的   （选填“A”、“B”或“C”）处。
（2）将电风扇调到最高档（最大风速），H调到最大值，此时H=120cm，它的放置状态如图乙所示，在水平方向扇叶受到空气对它向左的作用力F=16N，重力作用点P离电风扇底座中轴线横向距离a=15cm，P点离地面的距离b=40cm，底座半径r为17 cm。当电风扇的风速达到最大时，它会翻倒吗？请用杠杆平衡原理计算说明。（g=10N/Kg）
（3）电风扇在额定电压下工作，当旋转开关调到2位置时，风速档位是   （选填“低档”、“中档”或“高档”）；此时，电动机两端的电压为100V，求R₁的阻值及电动机的输出功率。

上海洋山港是全球最大的智能集装箱码头，图甲是将我国自行研制的大型桥吊从运输船上转运到正在建设中的洋山港码头时的情景。桥吊是码头上进行货物装卸的起重机，其简化示意图如图甲中所示，它由控制室、水平横梁 $\mathit{AB}$以及两个竖直的支架 $\mathit{CD}$和 $\mathit{EF}$组成。运输船中不同位置有数个密封的水舱，向这些水舱加水或减水，能保证牵引车将桥吊从运输船转运到码头的过程中，运输船的甲板始终保持水平且与码头的地面相平。

（1）牵引车将桥吊缓缓向右拖向码头时，支架 $\mathit{CD}$和 $\mathit{EF}$下的轮子会沿顺时针方向转动，请在图乙中画出支架 $\mathit{CD}$下的轮子对运输船甲板摩擦力的示意图。

（2）若牵引车拖行桥吊的功率是 $50\mathit{kW}$， $9s$内将桥吊沿水平方向匀速拖行了 $3m$，则这段时间内牵引车对钢缆的拉力是多少牛？

（3）已知桥吊的总质量是 $2200t$，支架 $\mathit{CD}$和 $\mathit{EF}$的高度均是 $50m$， $C$点到横梁 $A$端的距离是 $60m$， $E$点到横梁 $B$端的距离是 $18m$，桥吊的重心 $O$到横梁 $A$端和 $B$端的距离分别是 $72m$和 $28m$。试求牵引车将桥吊从图甲所示的位置拖到图丙所示的位置时，运输船的水舱中增加了多少立方米的水？

郝强同学对建筑工地上的长臂吊车（如图甲）有些疑惑：不吊物体它能平衡，吊重物也能平衡，重物沿臂移动仍能平衡．后来他通过设计“移动支点式杠杆”模型（如图乙）弄懂了类似问题：密度及粗细都均匀的直棒AB＝1.8m，放在一个宽度为40cm的凳子上，当在棒的A端固定一个铅块（忽略大小）m_铅＝2kg时，棒刚好绕O₁点有转动的趋势（AO₁＝30cm）．
（1）求棒的质量m_棒；
（2）当在P处挂一重物时（PB＝10cm），棒刚好绕O₂点有转动的趋势．求重物质量m_物及此时棒对O₂点的压力F（g取10N／kg）；
（3）当悬线带着重物缓慢向A端移动时，可以认为凳面上只有某点E（即新支点）对棒有支持力．回答：随着重物左移，E点将“左移”或“右移”还是“不动”？棒对E点的压力F_E是“变大”或“变小”还是“不变”？（不必说明理由）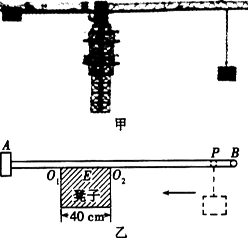

研究物理问题时，常需要突出研究对象的主要因素，忽略次要因素，将其简化为物理模型。

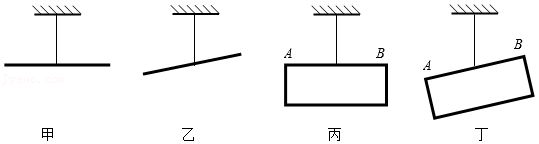
（1）如图甲，一质量分布均匀的杠杆，忽略厚度和宽度，长度不可忽略，用细线将它从中点悬起，能在水平位置平衡。将它绕悬点在竖直面内缓慢转过一定角度后（如图乙）释放，为研究其能否平衡，可将它看成等长的两部分，请在图乙中画出这两部分各自所受重力的示意图和力臂，并用杠杆平衡条件证明杠杆在该位置仍能平衡；

（2）如图丙，一质量分布均匀的长方形木板，忽略厚度，长度和宽度不可忽略，用细线将它从AB边的中点悬起，能在水平位置平衡。将它绕悬点在竖直面内缓慢转过一定角度后（如图丁）释放，木板在该位置能否平衡？写出你的判断依据。

阅读短文，回答问题．
无处不在的弹簧
　　弹簧在生活中随处可见，它在不同的领域发挥着重要作用．
　　弹簧的特点就是在拉伸或压缩时都要产生反抗外力作用的弹力，而且形变越大，产生的弹力越大；一旦外力消失，形变也消失．物理学家胡克研究得出结论：在弹性限度内，弹簧的形变量与它受到的拉力（或压力）成正比．
　　弹簧具有测量功能、紧压功能、复位功能和缓冲功能，以及储存能量的功能．弹簧在生产和生活中有许多应用，例如：制作弹簧测力计、钢笔套上的夹片、机械钟表的发条等．
（1）弹簧被拉伸或压缩时都产生反抗外力作用的弹力，这说明________．
（2）胡克的结论是________．
（3）下表是小明研究弹簧长度与所受拉力大小关系时记录数据的表格，空格中的数据是________．

钩码重／N	0	0.5	1.0		2.0	2.5
弹簧长度／cm	4	5	6	7	8	9

（4）举一个生活中应用弹簧的实例：________．（短文中实例除外）

已知滑动摩擦力大小与压力大小和接触面的粗糙程度有关，某实验小组在探究“滑动摩擦力大小与压力大小的关系”的实验中，使用的实验器材有弹簧测力计，木块（有挂钩）、长木板各一个，重为 $1N$的钩码若干。

（1）在长木板上用弹簧测力计沿水平方向拉动木块时，该同学判断弹簧测力计示数等于木块所受滑动摩擦力大小的依据是　      　

$A$．弹簧测力计示数是否稳定

$B$．木块是否做匀速直线运动

（2）该实验小组改变压力大小进行了多次实验，记录的实验信息和数据如表。

试验次数	1	2	3	4	5	6
接触面粗糙程度
压力 $F/N$	2	3	4	5	6	7
弹簧测力计示数 $P/N$	0.4	0.6	0.8	1.0	1.2	1.4
滑动摩擦力 $f/N$	0.4	0.6	0.8	1.0	1.2	1.4

根据表中的数据在图甲的方格纸上画出滑动摩擦力 $f$与压力 $F$的关系。

（3）分析图像得出的探究结论是　　        。

（4）该实验小组又选取了毛巾和棉布，在原有实验器材的基础上继续探究“滑动摩擦力大小与接触面粗糙程度的关系”实验中，某同学将毛巾平铺在长木板上，如图乙所示，在毛巾上用弹簧测力计水平拉木块时，发现木块下方的部分毛巾随木块一起由静止开始加速运动，便停止实验其他同学帮助他固定毛巾不动后，重新开始实验完成实验后，小组同学分析出部分毛巾随木块一起加速运动的原因是　     　。经讨论后发现还有其他的改进方法也可以解决毛巾随木块一起运动的问题，请写出你的改进方法　      　。

现有弹簧、钩码、直尺、指针等器材，小华要自制一个弹簧测力计，他首先测出弹簧的长度L₀＝2.10cm，然后在弹簧的下端挂上不同的钩码，测出弹簧的长度L，算出比原长L₀伸长的量ΔL（ΔL＝L－L₀），测量的数据如下表所示：

拉力F／N	1	2	3	4	5	6	7
长度L／cm	2.50	2.90	3.30	3.70	4.10	4.50	4.90
伸长量ΔL／cm	0.40	0.80	1.20	1.60	2.00	2.40	2.80

（1）从上表中的数据可以看出拉力F和弹簧伸长量ΔL的关系为：________．
（2）小华继续做实验，得到的数据如下表所示：

拉力F／N	8	9	10	11	12
长度L／cm	5.30	5.70	6.10	6.60	7.30
伸长量ΔL／cm	3.20	3.60	4.00	4.50	5.20

从上表所示的数据可以看出，拉力达到________N时，拉力和弹簧伸长量的关系就改变了．因此，弹簧测力计的测量范围只能达到________N．

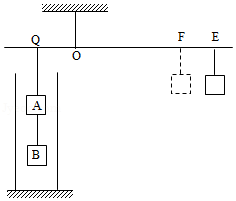
如图所示装置中，轻质杠杆支点为 $O$，物块 $A$、 $B$通过轻质细线悬于 $Q$点，当柱形薄壁容器中没有液体时，物体 $C$悬挂于 $E$点。杠杆在水平位置平衡；当往容器中加入质量为 $m_1$的水时，为使杠杆在水平位置平衡，物块 $C$应悬于 $F$点。 $A$． $B$为均匀实心正方体， $A$． $B$的边长均为 $a$。连接 $A$， $B$的细线长为 $b$， $B$的下表面到容器底的距离也为 $b$，柱形容器底面积为 $S$．已知： $a=b=2\mathit{cm}$， $S=16c{m}^2$， $O$、 $Q$ 两点间的距离为 $L_{\mathit{OQ}}=4\mathit{cm}$；三个物块的重为 $G_A=0.016N$． $G_B=0.128N$， $G_C=0.04N$， $m_1=44g$； ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$， $g=10N/\mathit{kg}$。杠杆重力对平衡的影响忽略不计，细线重力忽略不计，物块不吸水。

（1） $O$、 $E$两点间的距离 $L_{\mathit{OE}}=$？

（2） $E$、 $F$两点间的距离 $L_{\mathit{EF}}=$？

（3）如果剪断物块 $A$上方的细线，往容器中加水，直到容器中水的质量为 $m_2=120g$，则物块处于平衡位置后，水对物块 $B$上表面的压力 $F_b=$？

若某同学用一根弹簧制作弹簧测力计的实验时，在弹簧的下端挂不同重力的钩码，对应的弹簧的长度也不同，具体数据见下表：

钩码重力G/N	0	2	4	6	8	10	12
弹簧长度l/cm	3	4	5	6	7	8	8.5

(1)该同学制作的弹簧测力计的量程是_________N；
弹簧的原长是__________cm．
(2)请你分析表中这些实验数据,你得到的一个重要的实验结论是：
               ______________________________．
（3）某同学做《探索弹簧的弹力和伸长的关系》的实验时，他先把弹簧放在水平桌面上使其自然伸长，用直尺测出弹簧的原长为l₀，再把弹簧竖直悬挂起来，然后用竖直向下的力F拉弹簧下端，测出弹簧的长度为l，把l-l₀作为弹簧的伸长量x₀.这样操作，由于弹簧自身重力的影响，最后作出的F-x图象，可能是下图中_______图正确（其它操作都正确）

如图，均匀圆柱体A的底面积为6×10 ^{﹣ 3}m ²，圆柱形薄壁容器B的质量为0.3kg、底面积为3×10 ^{﹣ 3}m ²、内壁高为0.7m。把A、B置于水平地面上。已知A的密度为1.5×10 ³kg/m ³，B中盛有1.5kg的水。

（1）若A的体积为4×10 ^{﹣ 3}m ³，求A对水平地面的压力；

（2）求容器B对水平地面的压强；

（3）现将另一物体甲分别放在A的上面和浸没在B容器的水中（水未溢出），A对地面压强的变化量与B中水对容器底压强的变化量相等。

求：①物体甲的密度

②物体甲在B容器中受到的最大浮力。

我国第一高楼"上海中心大厦"的建筑高度是632米，为了避免台风来临时大厦上部剧烈晃动，大厦上部第125层安装了总质量上千吨的阻尼器系统，如图甲所示。阻尼器系统的钢索悬挂在大厦顶端，阻尼器类似一个质量巨大的金属摆，其简化模型如图乙所示。台风来临迫使大厦晃动，触发阻尼器产生与大厦晃动方向相反的摆动（如图丙所示）。阻尼器不停的往复摆动，使大厦上部晃动逐渐减弱，这样就不断吸收大厦晃动的能量。请回答下列问题：

（1）若阻尼器所在楼层距大厦底层高580m，乘坐高速电梯从底层到125层用时58s，则这一过程电梯的平均速度是多少？

（2）若阻尼器系统的质量是10 ⁶kg，则它受到的重力是多少？（取g＝10N/kg）

（3）图丙中，大厦刚开始向左晃动时，内部的阻尼器为什么会相对向右摆动？

（4）阻尼器吸收的能量不断增加，从安全角度考虑，设计时应使其摆动到最低点时速度不能过大，若在阻尼器下方加装铜质闭合线圈，结合电磁感应知识，你认为还缺少的器件是什么？请从能量转化的角度写出这一新增装置能减小摆动速度的原因。

今年5月，运用“蓝鲸一号”钻探平台，我国南海神孤海域首次实现可燃冰试采成功。

材料一：可燃冰，学名天然气水化合物，其化学式为 $C{H}_4·8H_{2}O$．它是天然气的固体状态（因海底高压）。埋于海底地层深处的大量有机质在细菌的分解作用下，最后形成石油和天然气（石油气），其中许多天然气被包进水分子中，在海底的低温 $(2~5^{°}\text{C})$与压力下结晶，形成“可燃冰”。

材料二：“蓝鲸一号”钻探平台设计和建造过程创新了多项世界记录。它长117米，宽92.7米，高118米，质量为42000吨。

请根据上述材料回答：

（1）形成可燃冰需要一定的生态环境。

①海底底层深处，这些分解有机质的细菌能很好的生存，体现了生物对环境的　　，这些细菌分解有机质　　（选填“需要”或“不需要” $)$氧气。这些细菌与真菌在细胞结构上的主要区别是　　。

②在开采过程中，极少量的垃圾废弃物没有对海洋环境造成破坏，这主要是因为海洋生态系统有　　的 能力。

（2）形成可燃冰的其中一个条件是有甲烷气源。

①可燃冰 $(C{H}_4·8H_{2}O)$中 $C:H:O$的元素质量比是　　。甲烷属于　　（选填“有机物”或“无机物” $)$

②与石油、煤等化石燃料相比较，开采可燃冰的积极意义有（写一条）　　。（可燃冰在空气中燃烧的化学方程式为 $C{H}_4\cdot 8H_{2}O+2O_2\frac{\underset{¯}{\mathit{点燃}}}{}C{O}_2+10H_{2}O)$

（3）如果南海海水的密度是 $1.03\times {10}^3$千克 $/$米 ${}^3$，“蓝鲸一号”钻探平台漂浮海面受到海水浮力是　　牛，浸入海水的体积至少需要　　米 ${}^3$，开采处的可燃冰可以直接在管口点燃，说明已经成为气体，从固体变成气体的原因可能是　　。

边长为 $20\mathit{cm}$的薄壁正方形容器（质量不计）放在水平桌面

上，将质地均匀的实心圆柱体竖直放在容器底部，其横截面积为 $200c{m}^2$，高度为 $10\mathit{cm}$。如图1所示。然后向容器内缓慢注入某种液体，圆柱体始终直立，圆柱体对容器底部的压力与注入液体质量的关系如图2所示。 $(g$取 $10N/\mathit{kg})$

（1）判断圆柱体的密度与液体密度的大小关系，并写出判断依据；

（2）当圆柱体刚被浸没时，求它受到的浮力；

（3）当液体对容器底部的压强与容器对桌面的压强之比为 $1:3$时，求容器内液体的质量。

如图甲所示是我们经常看到的场景，满载木材的货车，车厢尾部没有任何遮挡，一旦货车突然向前加速，木材就可能向后滑出，对后面的车辆造成严重伤害。这引起了小光的思考：只要货车加速，木材就都会滑出吗？

为此他请教了老师，老师解释道：这要看车加速的程度，物理学中用"加速度"这个物理量来描述物体加速的快慢程度，要让物体加速运动，就需要有外力对它作用。要使木材不滑落，必须有其他物体对它施加摩擦力，使它产生和车相同大小的加速度，与车保持相对静止，一起向前运动。

小光将以上情景简化成了如图乙所示的模型，水平车厢中有一根质量分布均匀的木头。

请你根据以上信息解答下列问题：

（1）若木头的质量为100kg，它的重力是多大？（取g＝10N/kg）

（2）若车厢长3m，木头长4m，在木头从车厢滑出的过程中，车厢对木头的摩擦力为100N，则这一过程中摩擦力至少对木头做了多少功？（提示：木头重心O在其中点处，当重心滑过车厢尾部，木头会倾倒）

（3）小光查阅资料得知：物体运动时加速度与外力的合力大小关系为： $a=\frac{F_{合}}{m}$ ，a表示加速度，其单位是m/s ²．若货车加速度为1.5m/s ²，请结合上述数据计算说明这根木头是否会滑落。

（4）在甲图场景中，若货车在水平路面上沿直线加速行驶，请指出车厢哪一部分木材最易滑落？并解释为什么另一部分不易滑落？

如图是某科技小组设计的一个提升重物的装置，CD是一个以O点为转轴的水平杠杆，CO：OD=3：2。滑轮组固定在杠杆C点，通过固定在水平地面的电动机匀速提升重物，每个滑轮的质量均为m₀。放置在水平地面上的配重E通过细绳竖直拉着杠杆D点，使杠杆CD始终保持水平平衡，配重E的质量m_E为100kg。当电动机用拉力F₁匀速提升重物A时，滑轮组的机械效率为η₁，物体A匀速上升的速度为v₁；当电动机用拉力F₂匀速提升重物B时，滑轮组的机械效率为η₂，物体B匀速上升的速度为v₂。在匀速提升重物A、B的过程中，电动机的功率保持不变。已知F₂-F₁=50N，v₁:v₂=5:4，η₂=90%。细绳和杠杆的质量、滑轮与轴的摩擦均忽略不计，g取10N/kg。求：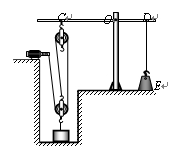

（1）拉力F₁的大小；
（2）滑轮组的机械效率η₁；
（3）当电动机用拉力F₂匀速提升重物B时，配重E对地面的压力N₂。