初中物理力和机械试题

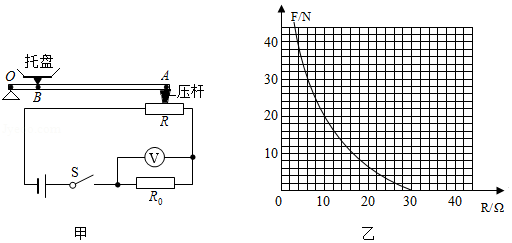
某物理研究小组设计了一个压力报警装置，工作原理如图甲所示。 $\mathit{OBA}$为水平杠杆， $\mathit{OA}$长 $100\mathit{cm}$， $O$为支点， $\mathit{OB}:\mathit{BA}=1:4$；已知报警器 $R_0$的阻值恒为 $10\Omega$，压力传感器 $R$固定放置，压力传感器受到的压力 $F$与 $R$的阻值变化的关系如图乙所示。当托盘空载时，闭合开关 $S$，电压表的示数为 $1V$：当托盘所受的压力增大，电压表的示数达到 $2V$时，报警器 $R_0$开始发出报警信号。托盘、压杆和杠杆的质量均忽略不计，电压表的量程为 $0~3V$．

求：

（1）电源电压；

（2）当报警器开始报警时，压力传感器受到的压力；

（3）当托盘受到的压力为 $120N$时，报警器是否报警；

（4）当电路输出的电功率与电路在安全状态下输出的最大电功率的比值为 $5:6$时，托盘受到的压力。

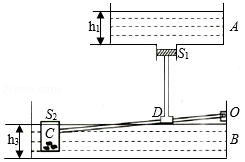
如图为某蓄水池的模拟原理图， $A$池中的液面高度 $h_1=10\mathit{cm}$，池底有一出水口，出水口下的活塞通过连杆与杠杆 $\mathit{OC}$相连，活塞横截面积

$S_1=1.2\times {10}^{-2}{m}^2$．杠杆可绕 $O$端上下转动，另一端有一中空且内有配重的圆柱形浮子浸入 $B$池中， $\mathit{DO}$是杠杆总长的 $\frac{1}{3}$，杠杆对浮子的作用力沿竖直方向。原设计当杠杆水平时，浮子浸入水深 $h_2=5\mathit{cm}$，活塞恰能堵住出水口。但在使用时发现，活塞离出水口尚有一小段距离时，浮子便不再上浮，此时浮子浸入水深 $h_3=8\mathit{cm}$。若将浮子的配重减少，△ $G=2.6N$，杠杆变为水平且活塞恰能堵住出水口。出水口面积略小于 $S_1$，计算时可认为相等，水的密度 ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$， $g=10N/\mathit{kg}$。（活塞与连杆自重、杠杆自重及所受浮力、两池中液面高度的变化均不计。 $)$

求：

（1） $A$池池底水深为 $h_1$处所受压强；

（2）活塞恰能堵住出水口时连杆对杠杆压力的大小；

（3） $B$池中浮子的横截面积 $S_2$。

如图13-4-4所示，等臂杠杆两端各挂一个质量相等的实心铁块和铝块（已知ρ_铁＞ρ_铝），杠杆平衡，若将它们同时浸没在水中，杠杆将（　　）

图13-4-4

A．仍平衡

B．左端下沉

C．右端下沉

D．无法判定

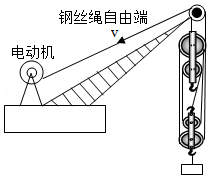
如图所示是打捞物体的模拟装置。现电动机带动钢丝绳自由端以 $0.5m/s$的速度匀速拉动滑轮组，经过 $5\mathit{min}$将体积为 $0.1m^3$的物体由海底提升到海面，物体离开海面后钢丝绳自由端的速度变为 $0.49m/s$，此时电动机的输出功率比物体在海水中时增大了 $12\%$（不计物体的高度、绳重和摩擦， ${\rho }_{物}=7.6\times {10}^3\mathit{kg}/m^3$， $g$取 $10N/\mathit{kg}$， ${\rho }_{\mathit{海水}}$取 $1.0\times {10}^3\mathit{kg}/m^3)$。求：

（1）物体浸没在海水中受到的浮力；

（2）物体在海底时的深度；

（3）物体在海底时受到海水的压强；

（4）物体在海面下匀速上升过程中，该滑轮组的机械效率（不计动滑轮体积）

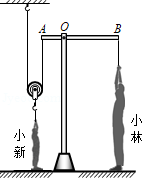
如图所示，站在水平地面上的小林想通过杠杆 $\mathit{AB}$ 和动滑轮拉起同样站在水平地面上的小新。杠杆 $\mathit{AB}$ 可绕转轴 $O$ 在竖直平面内转动，且 $\mathit{OA}:\mathit{OB}=1:2$ ，小林的质量 $m_1=50\mathit{kg}$ 。小新的质量 $m_2=48\mathit{kg}$ ，小新双脚与地面接触面积 $S=400c{m}^2$ 。当小林施加竖直向下的拉力 $F_1$ 时，小新未被拉动，此时小新对地面的压强 $p=2.5\times {10}^3\mathit{Pa}$ ，小林对地面的压强为 $p_1$ ；当小林施加竖直向下的拉力 $F_2$ 时，小新刚好被拉起，小林对地面的压强为 $p_2$ ，且 $p_1:p_2=16:15$ 。不计绳重，杠杆重力和一切摩擦， $g$ 取 $10N/\mathit{kg}$ 。求：

（1）小林施加拉力 $F_1$ 时，小新对地面的压力 $F_N$ ；

（2）动滑轮重力 $G_{动}$ 。

如图所示，杠杆AOB处在水平位置平衡，OA：OB＝1：2，浸入水中的铁球质量m＝7.9kg，加在B端的力F＝24.5N，ρ_铁＝7.9×10³kg/m³,g=10N/kg。则空心体积为：（    ）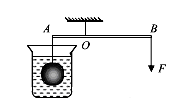

A．1×10^－3m^3。

B．2×10^－3m^3。

C．3×10^－3m^3。

D．4×10^－3m^3。

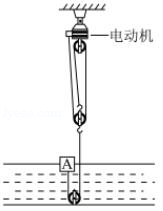
如图所示，实心物体 $A$漂浮在水面上，现利用电动机通过滑轮组拉动 $A$，使 $A$向下运动。已知 $A$的体积为 $1m^3$，密度为 $0.5\times {10}^3\mathit{kg}/m^3$．动滑轮重为 $1\times {10}^{3}N$，电动机工作时拉绳子的功率为 $1.2\times {10}^{3}W$且保持不变，不计绳重、摩擦和水的阻力，求：

（1） $A$的重力；

（2） $A$浸没在水中受到的浮力；

（3） $A$向下运动的最小速度；

（4） $A$向下运动过程中，滑轮组机械效率的最大值。

如图甲所示，滑轮组通过轻质弹簧悬挂于 $O$点，下端悬挂一柱形物体并浸没于装有水的柱形容器中，物体上表面恰好与水平面相平，绳子 $A$端固定，忽略滑轮重，绳重及摩擦。已知容器底面积为 $200c{m}^2$，水深 $20\mathit{cm}$，物体的底面积为 $100c{m}^2$，高为 $12\mathit{cm}$，重为 $24N$， ${\rho }_{水}=1.0\times {10}^3\mathit{kg}/m^3$， $g$取 $10N/\mathit{kg}$。

（1）求水对容器底的压强；

（2）求水对物体的浮力大小；

（3）求弹簧所受拉力的大小；

（4）若要使柱形物体有 $\frac{3}{4}$的长度露出水面，需打开阀门 $K$放出多少 $\mathit{kg}$的水？（题中弹簧所受拉力 $F$与其伸长量△ $x$的关系如图乙所示）

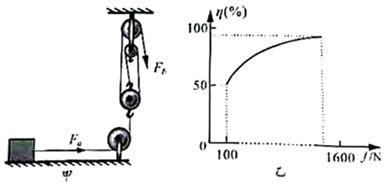
小熊在课外实践活动中，用如图甲所示的滑轮组匀速拉动放在树下一水平面上的不同物体，物体受到的摩擦力从 $100N$开始逐渐增加，每次物体被拉动的距离均为 $1m$。根据测量结果画出了该滑轮组机械效率与物体受到摩擦力大小变化的关系图象，如图乙所示。若不计绳重和绳与滑轮间的摩擦，求：

（1）由图乙可知，当物体受到的摩擦力为 $100N$时，滑轮组机械效率是多大？

（2）当滑轮组的机械效率为 $75\%$，物体以 $0.1m/s$的速度匀速运动时，该滑轮组的有用功率是多大？

（3）当物体与地面的摩擦力为 $1500N$时，体重为 $500N$的小熊竖直向下拉绳，还能用此滑轮组拉动物体吗？用计算结果说明。

图是某课外科技小组的同学设计的厕所自动冲水装置的示意图，它在自来水管持续供给的较小量的水储备到一定量后，自动开启放水阀门，冲洗厕所．实心圆柱体浮体A的质量为5.6kg，高为0.18m，阀门B的面积为7.5×10^﹣3m2；连接A、B的是体积和质量都不计的硬杆，长为0.16m．当浮体A露出水面的高度只有0.02m时，阀门B恰好被打开，水箱中的水通过排水管开始排出．已知水的密度为1×10³kg/m³，不计阀门B的质量和厚度．当水箱开始排水时，求：
（1）浮体A受到的重力；
（2）水对阀门B的压强和压力；
（3）浮体A受到的浮力；
（4）浮体A的密度．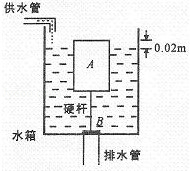

我国第一高楼"上海中心大厦"的建筑高度是632米，为了避免台风来临时大厦上部剧烈晃动，大厦上部第125层安装了总质量上千吨的阻尼器系统，如图甲所示。阻尼器系统的钢索悬挂在大厦顶端，阻尼器类似一个质量巨大的金属摆，其简化模型如图乙所示。台风来临迫使大厦晃动，触发阻尼器产生与大厦晃动方向相反的摆动（如图丙所示）。阻尼器不停的往复摆动，使大厦上部晃动逐渐减弱，这样就不断吸收大厦晃动的能量。请回答下列问题：

（1）若阻尼器所在楼层距大厦底层高580m，乘坐高速电梯从底层到125层用时58s，则这一过程电梯的平均速度是多少？

（2）若阻尼器系统的质量是10 ⁶kg，则它受到的重力是多少？（取g＝10N/kg）

（3）图丙中，大厦刚开始向左晃动时，内部的阻尼器为什么会相对向右摆动？

（4）阻尼器吸收的能量不断增加，从安全角度考虑，设计时应使其摆动到最低点时速度不能过大，若在阻尼器下方加装铜质闭合线圈，结合电磁感应知识，你认为还缺少的器件是什么？请从能量转化的角度写出这一新增装置能减小摆动速度的原因。

我国是世界上第一个成功完成海底沉船整体打捞工作的国家，图甲是起重工程船将“南海1号”沉船打捞出水的情况．为分析打捞工作，我们可以将实际打捞过程简化为如图乙所示的滑轮组竖直向上提升水中的金属物．已知正方体实心金属物的体积V=1×10-2m³，密度ρ_金=7.9×103kg/m³，ρ_水=1×103kg/m³，g=10N/kg，绳子重力不计．请问：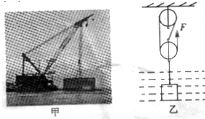

（1）若不计摩擦和滑轮重，当金属物始终浸没在水中时，需要多大的竖直向上拉力作用于绳子自由端才能将金属物匀速提升？
（2）若仍不计摩擦，但动滑轮重G₀=60N，要求在1min内将始终浸没在水中的金属物匀速提升6m，求绳子自由端竖直向上拉力的功率；
（3）若将金属物完全提出水面后继续向上匀速提升的过程中，该滑轮组的机械效率为94%，问作用于绳子自由端竖直向上的拉力是多大？（计算结果保留整数）

如图所示，将体积相同的物体G₁、G₂分别挂在杠杆的两端，杠杆处于平衡状态．若将两个物体G₁、G₂同时浸没在水中，则(　　)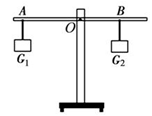

A．杠杆仍能保持平衡	B．杠杆不能平衡，A端下沉
C．杠杆不能平衡，B端下沉	D．无法确定杠杆的状态

如图是某装置利用浮力进行自动控制的原理图。AOB为一杠杆（质量忽略不计），OA ：OB="1" ：2。A端用细线挂一空心铝球，质量为2．7kg。当铝球一半体积浸在水中，在B端施加3．5 N的竖直向下的拉力F时，杠杆恰好在水平位置平衡。则铝球实心部分的体积为________m³，铝球受到的浮力为________N，铝球空心部分体积为________m³。（2．7×10³ kg／m³，g="10" N／kg）

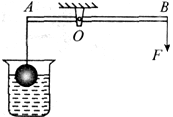
如图所示，是我校物理兴趣活动小组设计的一个健身器材，它是由一个质量为m₁长为2L的木棒和一个质量为m₂半径为R 的球体组成，同学们在活动中利用所学物理知识找出了该器材的重心。你能确定重心点O到A端的距离L₀吗？请推导并写出L₀与已知量的关系式。