如图甲是某中学科技小组设计的打捞水中物体的装置示意图。DB是以O点为转轴的水平杠杆,杠杆可以绕O点在竖直平面内转动,OD的长度为2m。水平地面上的配重E通过细绳竖直拉着杠杆D端,配重E的质量mE为250kg。安装在杠杆DB上的行走装置由支架、动滑轮X、提升电动机、定滑轮K构成,行走装置的质量m为20kg。电动机Q可以通过定滑轮S和动滑轮X拉动行走装置沿BO水平滑动。固定在提升电动机下的定滑轮K和动滑轮M组成滑轮组Y,当行走装置处于杠杆DB上C点的位置时,提升电动机拉动绳子H端,通过滑轮组Y竖直提升水中的圆柱体A。圆柱体A完全在水中,以0.1m/s匀速上升的过程中,滑轮组Y的机械效率为η1,配重E对地面的压强为p1;物体A以原来的速度匀速竖直上升,全部露出水面后,最终停在空中某高度时,配重E对地面的压强为p2。滑轮组Y提升物体A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置保持平衡。电动机H处绳子拉力的功率随时间变化的情况如图乙所示。已知圆柱体A的质量mA为60kg,底面积为30dm2,p1与p2之比为4∶1。物体A被打捞出水面后,停留在一定高度,电动机Q开始拉动行走装置。在行走装置以0.05m/s的速度水平匀速移动的过程中,电动机Q处拉力T的功率为5W,行走装置受到的水平拉力为F。细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg。
求:(1)动滑轮M所受的重力;(2)机械效率η1;(3)OC的长度;(4)拉力F。
如图所示,牵引车通过滑轮组匀速打捞起河水中的物体A,在被打捞的物体没有露出水面之前,牵引车控制绳子自由端,使物体A以0.5m/s的速度匀速上升,牵引车对绳的拉力为F1,拉力F1的功率为P1;当被打捞的物体完全露出水面后,牵引车控制绳子自由端,使物体A以0.3m/s的速度匀速上升,牵引车对绳的拉力为F2,拉力F2的功率为P2,且P1=P2。已知动滑轮重100N,物体完全露出水面后滑轮组的机械效率为80%(若不计摩擦、绳重及水的阻力,g取10N/kg),则被打捞的物体A的密度为 kg/m3。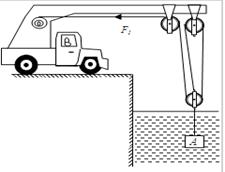
在生产玻璃过程中,常用位于天车上的卷扬机(其内部有电动机提供动力)通过滑轮组和真空吸盘提升玻璃,如图甲所示。当卷扬机通过滑轮组提升质量为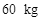 的玻璃并使玻璃以速度
的玻璃并使玻璃以速度 匀速上升时,卷扬对滑轮组绳端的拉力为
匀速上升时,卷扬对滑轮组绳端的拉力为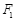 ,天车对卷扬机的支持力为
,天车对卷扬机的支持力为 ,拉力
,拉力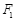 的功率为
的功率为 ,滑轮组的机械效率为
,滑轮组的机械效率为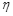 ;当卷扬机通过滑轮组提升质量为
;当卷扬机通过滑轮组提升质量为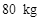 的玻璃并使玻璃以速度
的玻璃并使玻璃以速度 匀速上升时,卷扬机对滑轮组的拉力
匀速上升时,卷扬机对滑轮组的拉力 ,天车对卷扬机的支持力为
,天车对卷扬机的支持力为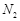 。已知拉力
。已知拉力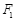 所做功随时间变化的图像如图乙所示,卷扬机的质量为
所做功随时间变化的图像如图乙所示,卷扬机的质量为 ,滑轮
,滑轮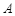 、
、 的质量均为
的质量均为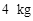 ,
,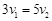 ,
,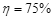 ,吸盘和绳的质量及滑轮与轴的摩擦均可忽略不计,
,吸盘和绳的质量及滑轮与轴的摩擦均可忽略不计,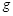 取
取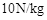 。求:
。求:
(1) 的大小;
的大小;
(2) 的大小;
的大小;
(3) 与
与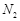 的比值。
的比值。
CCTV科教频道曾报道:有一辆小车载人后停在水平放置的地磅上时,左前轮、右前轮、左后轮、右后轮对地磅的压力分别为4750N,4980N,4040N,3960N.假设该小车四个轮子的轴心围成一个长方形,O为几何中心,AB、CD为两条对称轴,如图所示.若再在车上放一重物,能使整辆车所受重力的作用通过O点,则该重物的重心应落在
A.AOC区域上
B.BOC区域上
C.AOD区域上
D.BOD区域上
如图所示,一均匀杠杆A处挂2个钩码,B处挂1个钩码,杠杆恰好平衡,若每个钩码质量均为50g,在A、B两处再各加一个钩码,那么:( )
A.杠杆仍平衡
B.杠杆左边向下倾
C.杠杆右边向下倾
D.无法确定杠杆是否平衡
如图,用滑轮组从H=10米深的水中匀速提起底面积为0.04米2、 高2米的实心圆柱体,该物体的密度是2.5×103千克/米3。现在动滑轮挂钩用钢丝绳与该物体相连,已知绕在滑轮上的绳子能承受的最大拉力F为700牛。
⑴求该物体露出水面前所受的浮力。
⑵若不计摩擦、绳和动滑轮重,绳子被拉断时,物体留在水中的体积为多少立方米?
⑶若考虑摩擦、绳和动滑轮重,该装置的机械效率为90%,将物体匀速提升至露出水面前,拉力F做的功为多少焦?(g=10牛/千克)
如图16所示,直径为36cm的半球形碗固定在水平面上,碗的端口水平。一根密度分布均匀、长度为47cm的光滑杆ABC搁置在半球碗上,碗的厚度不计,杆平衡时碗内部分AB段与碗外部分BC段的长度之比为( )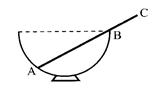
| A.38:9 | B.35:12 | C.32:15 | D.27:20 |
如图所示,密度分布均匀的圆柱形棒的一端悬挂一个小铁块并一起浸入水中。平衡时棒浮出水面的长度是浸入水中长度的n倍。若水的密度为ρ,则棒的密度为( )
A.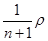 |
B. |
C. |
D.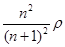 |
如图装置为某学生在科技创新大赛时发明的可以直接测量密度的“密度天平”。其制作过程如下:选择一根长1米杠杆,调节两边螺母使杠杆在水平位置平衡。在左侧离中点10厘米的A位置用细线固定一个质量为150克、容积为80毫升的容器。右侧用细线悬挂一质量为50克钩码(细线的质量忽略不计)。测量时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位置直接读出液体的密度。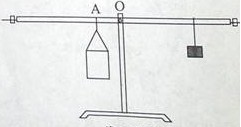
(1)该“密度天平”的“零刻度”应标在右端离支点O cm处。
(2)该“密度天平”的量程为多大?
(3)若将钩码的质量适当增大,该“密度天平”的量程将 (选填“增大”、“减小”或“不变”).
如图一均匀木板长12m,重200N,距A端3m处有一固定转轴O,另一端B用细绳悬吊着,使木板成水平状态.若细绳能承受的最大拉力为200N,细绳与木板的夹角为30°,欲使一个体重为600N的人在板上能安全行走,此人在板上行走的范围是多大?(求出离O点左侧多少米到离O点右侧多少米)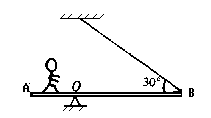
如图所示,轻质杠杆AD用两根软绳悬挂于天花板上,两绳分别系在杠杆上的B、C两点。已知杠杆的长度为0.8m,BC间的距离为0.2m,CD间的距离为0.2m。用细绳将滑轮组固定在杠杆的A端,物体E(其质量可变)挂在动滑轮的挂钩上,每个滑轮重均为60N。物体H通过细绳挂在杠杆的D端,其质量始终保持不变。为使杠杆AD保持水平平衡,滑轮组所能提升重物E的最大质量m1与最小质量m2之比为4:1。杠杆、细绳的质量及一切摩擦均可忽略不计,取g= 10N/kg。求: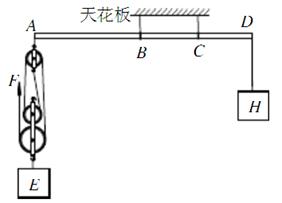
(1)滑轮组对杠杆A端的最大拉力FA1与最小拉力FA2之比;
(2)重物E的最大质量m1;
(3)滑轮组的最小机械效率。(百分号前保留整数)
如图甲所示,将一根质量分布均匀的金属硬棒的一端通过铰链固定在O点,并能使金属棒绕O点在竖直面内自由转动。现通过一个“拉力—距离传感器”可对硬棒施加一个竖直向上的力,使硬棒在水平位置始终保持平衡。已知硬棒的长度是1.2m,“拉力—距离传感器”可自动记录拉力F的大小和拉力作用点到O点的距离x,并将记录的结果输送到计算机绘制出F与x的关系图线。若计算机上显示出的拉力F与距离x倒数的变化关系如图乙所示,则可知金属棒所受的重力为 N。
弹簧测力计是测量力的大小的仪器,两个同学同时用F1=4N的力拉一弹簧测力计的两端,则弹簧测力计的示数为________N。若将此弹簧测力计的一端固定在墙上,另一端用F2=8N的力拉它,则弹簧测力计的示数为________N。
图中是小华利用杠杆提升浸没在水中的物体B的示意图。杠杆CD可绕支点O在竖直平面内转动,OC∶OD=1∶2,物体A为配重,其质量为200g。烧杯的底面积为75cm2,物体B的质量是320g,体积是40cm3。当物体B浸没在水中时,水对杯底的压强为p1。当用力拉A,将物体B从容器底提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉A的力为F,杯中水对容器底的压强为p2。若p1与p2之差为40Pa。则拉力F是___________N(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)。
试题篮
()