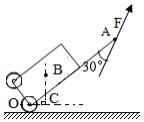
如图所示为一拉杆旅行箱的示意图将其视为杠杆, 为支点, 为重心, 为竖直方向, 为拉杆端点已知箱重为 , 为 , 为 。
(1)图中在 点沿图示方向施加动力 ,箱子静止则动力 的力臂为 ,大小为 。
(2)使拉杆箱在图示位置静止的最小动力为 。
(3)生活中,常把箱内较重物品靠近 点摆放,这样使拉杆箱在图示位置静止的最小动力将 (选填“变大”、“变小”或“不变” 。
从地面上搬起重物我们的常见做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?下面就建立模型说明这个问题。把脊柱简化为杠杆如图丙所示,脊柱可绕骶骨(轴 转动,腰背部复杂肌肉的等效拉力 作用在 点,其实际作用方向与脊柱夹角为 且保持不变,搬箱子拉力 作用在肩关节 点,在 点挂一重物代替箱子。用测力计沿 方向拉,使模型静止,可测出腰背部复杂肌肉拉力的大小。接着,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角 ,多次实验得出结论。

(1)在丙图中画出 力臂 。
(2)当 角增大时, (变大 不变 变小), (变大 不变 变小)。
(3)如果考虑到人上半身的重力,那么腰背部肌肉的实际拉力将比丙图中 要 (大 小)。
(4)对比甲乙两种姿势所对应丙图中的两种状态,由以下分析可得, (甲 乙)图中的姿势比较正确。
仔细阅读材料,根据材料提供的信息回答问题:
我们已经学过杠杆的力臂和杠杆的平衡条件,如果把这些知识稍加拓宽和延伸,就可尝试用新的方法来解决一些实际问题.有固定转动轴的物体在力的作用下处于静止或匀速转动的状态称为力矩平衡状态.物理学中把力和力臂的乘积叫做力对转动轴的力矩.力矩用M表示,即M=FL,式中L为力臂,力臂是转动轴到力的作用线的距离.在国际单位制中,力矩的单位是牛顿•米,符号为N•m.引入力矩概念后,杠杆的平衡条件可叙述为:
使杠杆沿顺时针转动的力矩与使杠杆沿逆时针转动的力矩相等.用公式表示为:M顺=M逆.
(1)力矩的表达式为:M= FL ,力矩的国际单位为 N•m .
(2)用垂直于门的力推门,推力F=80N,手到门轴的距离为0.3m,则F对门轴的力矩M为 24 N•m.
(3)如图所示,一根均匀木棒OA可绕过O点的水平轴自由转动,现有一方向不变的水平力F作用于该棒的A点,使棒从竖直位置缓慢转到偏角θ<90°的某一位置(缓慢转动可视为匀速转动),设M为力F对转轴的力矩,对此过程中M和F判断正确的是 A .(选填字母)
A.M不断变大,F不断变大 B.M不断变大,F不断变小
C.M不断变小,F不断变大 D.M不断变小,F不断变小

试题篮
()