初中物理探究杠杆的平衡条件实验计算题

郝强同学对建筑工地上的长臂吊车（如图甲）有些疑惑：不吊物体它能平衡，吊重物也能平衡，重物沿臂移动仍能平衡！后来他通过设计“移动支点式杠杆”模型（如图乙）弄懂了类似问题：密度及粗细都均匀的直棒AB=1.8m，放在一个宽度为40cm的凳子上，当在棒的A端固定一个铅块（忽略大小）m_铅=2kg时，棒刚好绕O₁点有转动的趋势（AO₁=30cm）．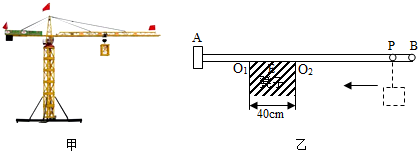

（1）求棒的质量m_棒；
（2）当在P处挂一重物时（PB=10cm），棒刚好绕O₂点有转动的趋势．求重物质量m_物及此时棒对O₂点的压力F（g取10N/kg）；
（3）当悬线带着重物缓慢向A端移动时，可以认为凳面上只有某点E（即新支点）对棒有支持力．回答：随着重物左移，E点将“左移”或“右移”还不“不动”？棒对E点的压力F_E是“变大”或“变小”还是“不变”？（不必说明理由）

如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的，求：甲、乙两个物体的质量之比．

杆秤是用来测量物体质量的工具，也是我国劳动人民智慧的结晶。如图所示，杆秤的提纽到挂钩的距离OA＝4cm，当秤砣移动到离提纽的距离为20cm时，杆秤刚好水平平衡，若秤砣的质量为0.6kg，求：

（1）所称物体的质量是多少kg？
（2）若用质量为0.5kg的秤砣去测量该物体，当杆秤刚好水平平衡时秤砣移动到离提纽的距离为多少cm？

郝强同学对建筑工地上的长臂吊车（如图甲）有些疑惑：不吊物体它能平衡，吊重物也能平衡，重物沿臂移动仍能平衡！后来他通过设计“移动支点式杠杆”模型（如图乙）弄懂了类似问题：密度及粗细都均匀的直棒AB=1.8m，放在一个宽度为40cm的凳子上，当在棒的A端固定一个铅块（忽略大小）m_铅=2kg时，棒刚好绕O₁点有转动的趋势（AO₁=30cm）．

（1）求棒的质量m_棒；
（2）当在P处挂一重物时（PB=10cm），棒刚好绕O₂点有转动的趋势．求重物质量m_物及此时棒对O₂点的压力F（g取10N/kg）；
（3）当悬线带着重物缓慢向A端移动时，可以认为凳面上只有某点E（即新支点）对棒有支持力．回答：随着重物左移，E点将“左移”或“右移”还不“不动”？棒对E点的压力F_E是“变大”或“变小”还是“不变”？（不必说明理由）

如图所示，质量为8kg，边长为5cm的正方体物块A置于水平地面上，通过细绳系于轻质杠杆BOC的B端，杠杆可绕O点转动，且CO=3BO，在C端用F=20N的力竖直向下拉杠杆，使杠杆在水平位置平衡．（绳重不计，g取10N/kg）

求：（1）物体A的重力G；
（2）B端细绳的拉力F_拉；
（3）物体A对地面的压力F_压；
（4）物体A对地面的压强P．

AC为轻杆，杆始终保持水平，O为支点，OA=OC=25cm，CD⊥OC，AB绳与水平方向成30°角，即∠OAB=30°，AB绳所能承受的最大拉力为10N．

（1）当烧杯中未装入水时，求D端所悬挂重物的最大重力为多少？
（2）当烧杯中装入水时，重物浸没在水中，已知所悬挂重物体积为125cm³，ρ_水=1.0×10³kg/m³，求此时D端所悬挂重物的最大重力又为多少？（g=10N/kg）

如图所示，质量不计的光滑木板AB长1.2m，可绕固定点O转动，离O点0.2m的B端挂一重物G，板的A端用一根与水平地面成30°夹角的细绳拉住，木板在水平位置平衡时绳的拉力是6N．然后在O点的正上方放一质量为0.3kg的小球，若小球以25cm/s的速度由O点沿木板向A端匀速运动，问小球至少运动多长时间细绳的拉力减小到零．（取g=10N/kg，绳的重力不计）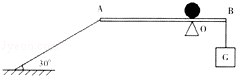

有一电热水器，质量为20kg，装满水后的总质量为70kg，该热水器额定电压是220V，内部有两个加热管，有三档不同的加热功率，其中最大额定功率是2000W，如图是电热水器安装的尺寸及其受力示意图，在竖直方向上热水器受到挂钩拉力F₂和重力G，在水平方向上热水器受到膨胀螺钉对它的拉力F₁和墙壁对它的支持力F₃．（g取10N/kg，ρ_水=1.0×103kg/m3）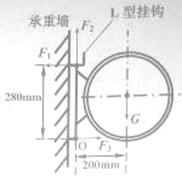

（1）该热水器最多能装多少立方米的水？
（2）该热水器装满水时，膨胀螺钉的拉力F₁是多大？
（3）若热水器内部两个加热管的电阻阻值相同，则每个加热管的电阻是多少？

小雯设计了一个测量物体重力的“托盘秤”，如图是原理示意图，其中的托盘用来放置被测物体，OBA是可绕O点转动的杠杆，R₁是压力传感器（其电阻值会随所受压力大小变化而变化，变化关系如下表），R₀为定值电阻,为显示重力大小的仪表（实质是一个量程为0—3V的电压表）。已知OB:OA=1:2，R₀=100Ω，电源电压恒为3V（忽略托盘、杠杆及压杆的重力）。

压力F/N	0	50	100	150	200	250	300
电阻R1/Ω	300	250	200	150	100	50	0

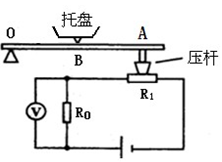
(1)托盘上没放物体时，压力传感器R₁的电阻值是  ______ Ω。
(2)当托盘上放被测物体时，电压表的示数如图所示，则此时压力传感器R₁上的电压是多少？

(3)第(2)题中被测物体的重力是多少？

某兴趣小组制作了一个测量质量的电子秤，其原理如图甲所示，它主要四部分构成：托板、压力杠杆OAB、压敏电阻R（电阻值会随所受压力大小发生变化的可变电阻）和显示重力大小的仪表A（实质是量程为0～0.6A的电流表），其中OA长5cm，AB长20cm，电源电压恒为9V，压敏电阻R的阻值与所受压力的关系如图乙所示（托板和杠杆组件的质量可以忽略不计，g取10N/kg）。求：

（1）托板上放某一重物时，电流表示数为0.2A，电子秤在1min内消耗的电能；
（2）托板上没有放置物体时，电路中的电流；
（3）为保护电流表不被损坏，电子秤能测量的最大质量。

某电开水器的结构如图甲所示（剖面图），简化的内部电路如图乙所示，进水管管口的阀门由轻质浮子1和与它们相连的两根轻质硬杆控制，只有进水管中的水压在正常范围内，冷水箱和煮水箱中的水位就比出水管管口低，冷水不会从出水管流出。当冷水箱中的水位达到一定高的时，浮子2浮起，会触动单刀三掷开关S₁，煮水电热管R₁通电发热，冷水被煮沸，水面升高，开水就从出水管进入贮水箱，当贮水箱中水位达到一定高度时，浮子3浮起，又会触动单刀三掷开关S₁，煮水暂停，一旦贮水箱中水温下降使温控开关S₂闭合，保温电热管R₂就会通电发热，开水处于保温状态。

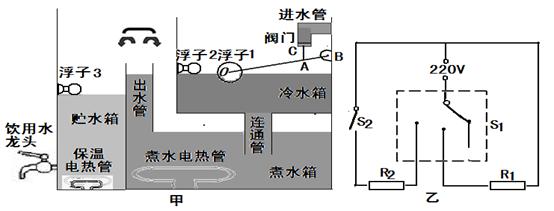
（1）已知煮水电热管R₁的阻值为12.1Ω，保温电热管R₂的阻值为48.4Ω，求电开水器的最大发热功率。
（2）图甲中，当浮子1上升到最高处后，它的最上端恰好和出水管管口相平，阀门就会将进水管管口关闭，此时AC杆沿竖直方向。已知浮子1的体积V=2.5×10^-4m³，进水管管口和阀门的横截面积S均为1×10^-4m²（不计阀门的质量、管壁的厚度及两者之间的摩擦）；BO∶BA=20∶1（O为轻质浮子1的球心、A为两轻质硬杆的相交处，B为轻质硬杆BO的转轴），水箱内水面上方的气压P₀=1×10⁵Pa。为了不让冷水直接进入贮水箱，进水管管口阀门的上表面受到的压强不能超过多少Pa?

小明做俯卧撑时（如图23所示），可将其视为一个杠杆，重心在O点。他将身体撑起时，地面对两脚尖的支持力为250N，两脚尖与地面的接触面积为60cm²，双手与地面的接触面积为300cm²。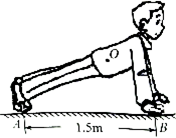

⑴画出以B为支点时重力的力臂L。
⑵如果小明的两脚尖对地面的压强与双手对地面的压强之比为5∶2，地面对双手的支持力为多少？
⑶小明在1min内做了30个俯卧撑，每次肩部上升的距离都为0.36m，则他1min内克服重力所做的功为多少?

甲、乙是两个完全相同的均匀实心圆柱体，重力都为5.4N。甲放在水平地面上，细绳的一端系于圆柱体甲上表面的中央，另一端竖直拉着轻质杠杆的A端。当把圆柱体乙悬挂在杠杆的B端时，杠杆在水平位置平衡，且AO︰B=2︰，如图a所示，此时甲对地面的压强为1350 Pa；当把圆柱体乙放入底面积为30 cm²的薄壁圆柱形容器M中，将质量为450g的水注入容器，圆柱体乙刚好有3/4体积浸在水中，水在容器中的深度为20cm，如图b所示。（已知ρ_水=1.0×10³kg/m³）求：
       
⑴圆柱体甲的底面积是多少cm²？
⑵当圆柱体乙刚好有3/4体积浸在水中时，所受到的浮力是多少N?
⑶圆柱体甲的密度是多少kg/m³？

．如图所示，斜面长S＝6m，高h＝2.lm．用沿斜面方向50N的推力F，在10s内将一个重为100N的物体由斜面底端匀速推到顶端．求：

（1）推力F的功率：
（2）运动过程中物体克服摩擦力所做的功：
（3）斜面的机械效率．

小明同学设计的“风力测试仪”在校科技节上备受师生们的青睐，“风力测试仪”的原理如图所示．电源电压6V，R₀为保护电阻，AB为长20cm、阻值为50W的均匀电阻丝．OP为质量、电阻均不计的金属细杆，下端连接一个重为2N的球P．闭合开关S，无风时，OP下垂并与电阻丝的B端接触；有风时，球P受风力的作用，使金属细杆OP绕悬挂点O偏转，当偏转到电阻丝的A端时，电流表示数为0．6A．已知悬挂点O与电阻丝B端的距离为10cm，金属细杆OP始终与电阻丝AB接触良好且无摩擦，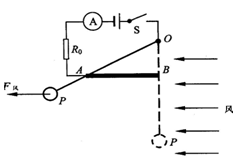

求：（1） R₀的阻值；
（2）无风时电流表示数；
（3）在风力作用下，当金属细杆OP在图示位置静止时，作出F风的力臂，并求出该力的大小．