由于流体具有粘滞性,因而物体在流体中运动要受到流体的阻力.科学家们已测得半径为R的球在流体中以速度v 运动时受流体阻力大小为F=6πηRv,其中η为流体的黏滞系数,不同流体η不同,它由流体的性质决定.某课外兴趣小组在研究性学习活动中为了测定某种流体的黏滞系数,设计如下实验:让密度为ρ=1.2×103 kg/m3半径为R=3cm的实心球在密度为ρ0=0.8×103 kg/m3的透明液体中竖直下落,发现球先加速下落后匀速下落,该兴趣小组的同学用频闪摄影的方法测出球匀速下落时的速度为v=4.9m/s.若球的体积计算式为V=4πR3/3,g=9.8N/kg.则该流体的黏滞系数η为( )
| A.0.16N•s/m | B.0.48N•s/m | C.0.16N•s/m2 | D.0.48N•s/m2 |
柱状容器内放入一个体积大小为200cm3的柱状物体,现不断向容器内注入水,并记录水的总体积V和所对应的水的深度h,如下表所示,则下列判断中不正确的是 

A.物体的底面积 为8cm2 为8cm2 |
B.容器的底面积 为12cm2 为12cm2 |
| C.物体的密度为0.7×103kg/m3 | D.物体所受到的最大浮力为1.4N |
甲、乙两个圆柱体(ρ甲<ρ乙)分别置于水平地面上,它们的底面积分别为S甲和S乙,高度分别为h甲和h乙.若均沿水平方向将两圆柱体截去相等的质量,使剩余部分对地面的压强p甲>p乙,则甲、乙两个圆柱体被截去前的情况可能是图中的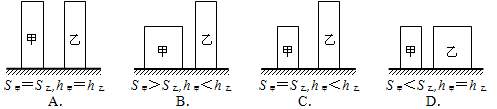
如图所示,边长为a、密度均匀的正方体物块静止于河岸边,在BB′边上施加一个力F使其绕DD′边转动掉落于河水中,它漂浮时露出水面的高度为h,水的密度为ρ,则下列说法中正确的是( )
A.物块的密度为 |
| B.物块的重力为(a﹣h)ρga |
| C.物块漂浮在水面时底面受水的压强为ρg(a﹣h) |
D.为了使物块掉落于河水中,力F至少是 |
小博想模拟同一艘轮船在海洋和河流中的沉浮情形.她将小铁块B固定在木块A上面代表“轮船”.用相同烧杯盛装等质量的水和盐水代表“河流”和“海洋”,放在水平桌面上,如图所示.第一次将AB放在水中,发现A的上表面恰好与液面相平;第二次放在盐水中,发现A的上表面露出了液面.则下面说法正确的是( )
| A.由模拟实验可知,轮船由河流航行到海洋将下沉 |
| B.AB在水中悬浮,在盐水中漂浮 |
| C.AB在水中所受的浮力大于在盐水中所受的浮力 |
| D.两烧杯底部所受液体的压力相等 |
如图所示,底面积不同的圆柱形容器A和B分别盛有甲、乙两种液体,两液面相平且甲液体的质量大于乙液体的质量.则此时液体对各自容器底部的压强pA、pB和液体对各自容器底部的压力FA、FB的关系是( )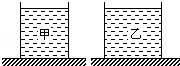
| A.pA<pB,FA=FB | B.pA<pB,FA>FB | C.pA>pB,FA=FB | D.pA>pB,FA>FB |
甲、乙两容器内盛有水,水对容器底部的压强分别为p甲和p乙.当水温从80℃降低到20℃时,则p甲和p乙的变化情况是( )
| A.p甲变小,p乙不变 | B.p甲不变,p乙变小 | C.p甲和p乙均变小 | D.p甲和p乙均不变 |
如图所示,桌面上是两个完全相同的圆柱形平底杯子,里面分别盛有质量相等的水和酒精, 两点到杯子底部的距离相等。已知水的密度
两点到杯子底部的距离相等。已知水的密度 kg/m3,酒精的密度
kg/m3,酒精的密度 kg/m3,则
kg/m3,则 两点的压强PA、PB的大小关系是:
两点的压强PA、PB的大小关系是:
| A.PA>PB | B.PA<PB | C.PA=PB | D.无法确定 |
如图所示,甲图中圆柱形容器中装有适量的水。将密度均匀的木块A放入水中静止时,有2/5的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300 Pa。若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa。若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1∶m2=5∶1,则下列说法中错误的是 
| A.木块A的质量mA与m1之比为1:3 |
B.在丁图中,液体的密度为 kg/m3 kg/m3 |
C.木块A的密度为 kg/m3 kg/m3 |
| D.在图丙中,木块A露出水面的体积与木块A的体积之比是1:5 |
把弯成“冂”形的玻璃管穿过软木塞分别插入两个大小相同的烧瓶内,如图所示.当玻璃管中着色水柱由静止向右移动时,不可能发生的情形是( )
| A.甲烧瓶中空气温度升高,乙烧瓶中空气温度不变 |
| B.甲烧瓶中空气温度降低,乙烧瓶中空气温度不变 |
| C.甲、乙两烧瓶中空气温度都升高 |
| D.甲、乙两烧瓶中空气温度都降低 |
由于流体具有粘滞性,因而物体在流体中运动要受到流体的阻力.科学家们已测得半径为R的球在流体中以速度v 运动时受流体阻力大小为F=6πηRv,其中η为流体的黏滞系数,不同流体η不同,它由流体的性质决定.某课外兴趣小组在研究性学习活动中为了测定某种流体的黏滞系数,设计如下实验:让密度为ρ=1.2×103 kg/m3半径为R=3cm的实心球在密度为ρ0=0.8×103 kg/m3的透明液体中竖直下落,发现球先加速下落后匀速下落,该兴趣小组的同学用频闪摄影的方法测出球匀速下落时的速度为v=4.9m/s.若球的体积计算式为V=4πR3/3,g=9.8N/kg.则该流体的黏滞系数η为( )
| A.0.16N•s/m | B.0.48N•s/m | C.0.16N•s/m2 | D.0.48N•s/m2 |
如图所示的容器,其下部横截面积S2为上部横截面积S1的3倍,当由管口注入重为G的某种液体时,上部液柱与容器的下部等高.则液体对容器底部的压力为( )
| A.(3/2)G | B.G |
| C.(3/4)G | D.(1/2)G |
将甲、乙两个完全相同的溢水杯放在水平桌面上,甲溢水杯中装满密度为ρ1的液体,乙溢水杯中装满密度为ρ2的液体。如图8甲所示,将密度为ρA,重为GA的物块A轻轻放入甲溢水杯中,物块A漂浮在液面上,并且有1/4的体积露出液面,液体对甲杯底的压强为P1。如图乙所示,将密度为ρB,重为GB的物块B轻轻放入乙溢水杯中,物块B沉底,物块B对乙溢水杯底的压力为F,液体对乙溢水杯杯底的压强为P2。已知
ρ1∶ρ2=3∶2,ρA∶ρB=4∶5,则下列说法中正确的是
| A.ρ1∶ρA,=3∶4 |
| B.FA浮∶FB浮=9∶8 |
| C.P1∶P2=2∶3 |
| D.F∶GB=13∶45 |
如图甲是一个底面为正方形、底面边长l=20cm的容器。把盛有h=10cm深的某种液体的容器放在水平桌面上,然后将边长a=b=10cm、c=12cm的均匀长方体木块放入这种液体中(液体未溢出),木块漂浮在液面上,此时木块底面受到液体向上的压力为7.2 N,容器底受到的液体压强为980Pa(g取10N/kg),由以上条件可以得出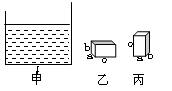
| A.液体的密度为0.98×103kg/m3 |
| B.木块漂浮在液面上时,容器中液体的深度为12.2cm |
| C.以图乙所示方式将木块放入液体中静止时,木块浸入液体中的深度为7.5cm |
| D.以图丙所示方式将木块放入液体中静止时,木块下表面离容器底的距离是4.75cm |
如图所示:木块浸没在水中,细线对木块的拉力是1N,剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加0.5N向下的压力,木块有20cm3的体积露出水面,则木块的密度为( )。
| A.0.6×103kg/m3 | B.0.7×103kg/m3 |
| C.0.8×103kg/m3 | D.0.9×103kg/m3 |
试题篮
()