初中物理压强和浮力计算题

如图所示，底面积为2×10^（2米²的圆柱形平底薄壁水槽放在水平地面上，一装有金属球的小盆漂浮在水槽的水面上，小盆的质量为1千克，金属球的质量为1.6千克，金属球的体积为0.2×10^（3米³。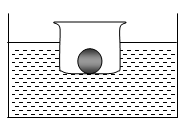

①　若把金属球从盆中拿出并放入水槽中后，小球沉入水底，求容器对水平地面压强的变化量。
②　求水对水槽底部的压强变化量。

如图，用滑轮组从H=10米深的水中匀速提起底面积为0.04米²、 高2米的实心圆柱体，该物体的密度是2.5×10³千克/米³。现在动滑轮挂钩用钢丝绳与该物体相连，已知绕在滑轮上的绳子能承受的最大拉力F为700牛。

⑴求该物体露出水面前所受的浮力。
⑵若不计摩擦、绳和动滑轮重，绳子被拉断时，物体留在水中的体积为多少立方米？
⑶若考虑摩擦、绳和动滑轮重，该装置的机械效率为90%，将物体匀速提升至露出水面前，拉力F做的功为多少焦？（g=10牛/千克）

如图所示，体积相等、密度分别为的ρ_A、ρ_B的A、B两个立方体正对叠放在水平桌面上，且ρ_A：ρ_B=1：3．A对B的压强为p_A，B对桌面的压强为p_B．

①如果A的体积为1.0×10^﹣3米³，密度为3×10³千克/米³，求A的质量、A对B的压强．
②如果逐渐减小A的体积，但始终保持A的形状为立方体且密度不变，在A的体积逐渐减小的过程中，列出p_A与p_B的比值的表达式，并指出比值的变化规律．

如图所示，某工程队在一次施工作业中，以恒定速度沿竖直方向将质量为5×10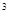kg的圆柱形实心工件从深水中吊起至距水面某一高度。绳子作用在工件上端的拉力F的功率P随工件上升高度h变化的图象如右图所示，不计水的阻力（ρ水＝1.0×10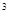kg/m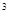,g取10N/kg），求：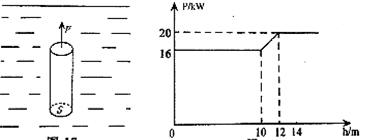

⑴工件上升的速度大小？
⑵当工件露出水面的1/2时所受的浮力大小？
⑶工件的横截面积S是多大？

我们已经知道，肺活量是一个人做最大吸气后再做最大呼气所呼出的气体的体积，单位是毫升（ml）．肺活量是身体机能的重要指标之一，对青少年的成长及日后身体是否健康都关系重大．我们要注意增强自身的肺活量．如图所示是一种测定肺活量的实用方法．图中A为倒扣在水中的开口薄壁圆筒（圆筒壁体积忽略不计），测量前排尽其中的空气（即测量前筒内充满水）．测量时，被测者吸足空气，再通过B尽量将空气呼出，呼出的空气通过导管进入A内，使A浮起．测得圆筒质量为m，横截面积为S，筒底浮出水面的高度为H，大气压强为p₀，水的密度为ρ_水，求：
（1）此时圆筒内空气的体积．
（2）筒内气体的压强．
（3）“肺活量体重指数”是人体重要的呼吸机能指数，它主要通过人体的肺活量与体重的比值来反映肺活量和体重的相关程度，用以对不同年龄、性别的个体与群体进行客观的定量比较分析．
肺活量体重指数=，单位是ml/kg；
例如，我国初三年级男学生肺活量体重指数标准：67以上为优秀；50～66为良好；33～49为及格；32以下为不及格．如果体重60kg的小强用上面的肺活量测试仪测肺活量，测得H=18cm，已知筒A的质量为200g，横截面积为200cm²，请计算他的肺活量体重指数是多少？

图的装置主要由长木板甲、物块乙和丙、定滑轮S和动滑轮P、水箱K、配重C和D及杠杆AB组成。C、D分别与支架固连在AB两端，支架与AB垂直，AB可绕支点O在竖直平面内转动。C通过细绳与P相连，绕在P上的绳子的一端通过固定在墙上的S连接到乙上，乙的另一端用绳子通过固定在桌面上的定滑轮与丙连接，乙置于甲上，甲放在光滑的水平桌面上。已知C重100N，D重10 N，丙重20N，OA:OB＝1:2，在物体运动的过程中，杠杆始终保持水平位置平衡。若在D上施加竖直向下F₀=20N的压力，同时在甲的左端施加水平向左的拉力F，甲恰好向左匀速直线运动，乙相对桌面恰好静止；若撤去拉力F改为在甲的右端施加水平向右的拉力F＇时，甲恰好在桌面上向右匀速直线运动，要继续保持乙相对桌面静止，则此时在D上施加竖直向下的压力为F₁；若移动K，将丙浸没水中，在拉力F＇作用下，甲仍向右匀速直线运动且乙相对桌面静止，则此时在D上施加竖直向下的压力为F₂。已知ρ_丙=2×10³kg/m³，F₁:F₂=4:5。杠杆、支架和不可伸缩细绳的质量、滑轮与轴的摩擦、杠杆与轴的摩擦均忽略不计。g取10N/kg。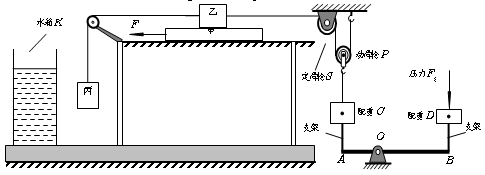

求：（1）丙浸没水中后受到的浮力F_浮；
（2）拉力F。

图是某课外科技小组的同学设计的厕所自动冲水装置的示意图，它在自来水管持续供给的较小量的水储备到一定量后，自动开启放水阀门，冲洗厕所．实心圆柱体浮体A的质量为5.6kg，高为0.18m，阀门B的面积为7.5×10^﹣3m²；连接A、B的是体积和质量都不计的硬杆，长为0.16m．当浮体A露出水面的高度只有0.02m时，阀门B恰好被打开，水箱中的水通过排水管开始排出．已知水的密度为1×10³kg/m³，不计阀门B的质量和厚度．当水箱开始排水时，求：
（1）浮体A受到的重力；
（2）水对阀门B的压强和压力；
（3）浮体A受到的浮力；
（4）浮体A的密度．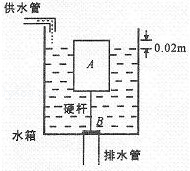

某提升装置中，杠杆AB能绕固定点O在竖直平面内转动，水平地面上的配重乙通过细绳竖直拉着杠杆B端。已知AO：OB=2：5，配重乙与地面的接触面积为S且S=200cm²。当在动滑轮下面挂上重1000N的物体甲静止时（甲未浸入水中），竖直向下拉绳子自由端的力为T₁，杠杆在水平位置平衡，此时配重乙对地面的压强为P₁且P₁=3.5×10⁴Pa；如果在动滑轮下挂一个质量为动滑轮质量5倍的物体丙，并把物体丙浸没在水中静止时，如图22甲所示，竖直向上拉绳子自由端的力为T₂，杠杆在水平位置平衡。此时配重乙对地面的压强为P₂且P₂=5.6×10⁴Pa。已知物体丙的质量与体积的关系的图像如图乙所示，如果不计杠杆重、绳重和滑轮轴间摩擦，图中两个滑轮所受重力相同取g=10N/kg。配重乙的体积为5×10^-2m³，求配重乙的密度。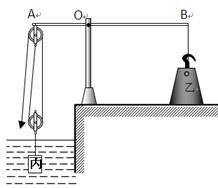

甲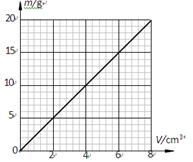

乙

如图是油压千斤顶的示意图，大活塞的直径是小活塞直径的5倍，大活塞上的重物G=5×10³牛，O为支点，AB∶OB=3∶1。要将重物G举起来，至少在A端加多大的力？不计摩擦。

制潜水艇模型如图1—5—16所示，A为厚壁玻璃广口瓶，瓶的容积是V₀，B为软木塞，C为排水管，D为进气细管，正为圆柱形盛水容器．当瓶中空气的体积为V₁时，潜水艇模型可以停在液面下任何深处，若通过细管D向瓶中压入空气，潜水艇模型上浮，当瓶中空气的体积为2 V_l时，潜水艇模型恰好有一半的体积露出水面，水的密度为恰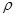_水 ，软木塞B，细管C、D的体积和重以及瓶中的空气重都不计．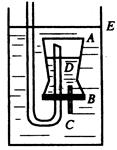

图1—5—16
　　求：（1）潜水艇模型．的体积；
　　（2）广口瓶玻璃的密度．

水平桌面上竖直放置一个底面积为S的圆柱形容器，内装密度为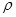₁的液体．将挂在弹簧测力计下体积为V的金属浸没在该液体中（液体未溢出）．物体静止时，弹簧测力计示数为F；撤去弹簧测力计，球下沉并静止于容器底部，此时液体对容器底的压力为容器底对金属球的支持力的n倍．
　　求（1）金属球的密度；（2）圆柱形容器内液体的质量．

工作人员用如图所示装置把水质监控仪器放入水中。第一次使仪器A在水中匀速上升的过程中（A未露出水面），人对绳子竖直向下的拉力为F₁，绳端的速度为v₁，机械效率为η₁；第二次把仪器B固定在A下方，A和B在水中匀速上升的过程中（A未露出水面），人对绳子竖直向下的拉力为F₂，绳端的速度为v₂，机械效率为η₂；η₁: η₂=34:35。已知V_A=V_B=3×10^-3m³， G_A=3G_B，G_B=50N。拉力F₁、F₂做功随时间变化的图像分别如图中①、②所示。（不计绳重、滑轮与轴的摩擦及水的阻力，g取10N/kg）

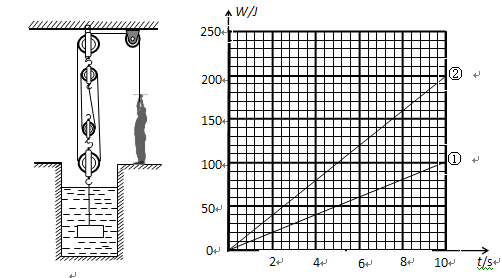
求：（1）A所受的浮力F_浮；
（2）动滑轮的重G_动；
（3）求v₁、v₂的比值。

如图所示，实心均匀正方体A、B放置在水平地面上，它们的高度分别为0.2米和0.1米，A的密度为2×10³千克/米³，B质量为1千克。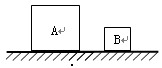

求：①A的质量；   ②B对水平地面的压强；
③若在正方体A、B上沿竖直方向按相同比例n截下一部分，并将截下的部分分别叠放在对方剩余部分上，这时A、B剩余部分对水平地面的压强为p_A′、p_B′，请通过计算比较它们的大小关系及其对应的比例n的取值范围。