阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点 , , , ,可通过构造直角三角形利用图1得到结论: 他还利用图2证明了线段 的中点 的坐标公式: , .

(1)请你帮小明写出中点坐标公式的证明过程;
运用:(2)①已知点 , ,则线段 长度为 ;
②直接写出以点 , , , 为顶点的平行四边形顶点 的坐标: ;
拓展:(3)如图3,点 在函数 的图象 与 轴正半轴夹角的平分线上,请在 、 轴上分别找出点 、 ,使 的周长最小,简要叙述作图方法,并求出周长的最小值.
在平面直角坐标系 中,对于不在坐标轴上的任意一点 ,我们把点 , 称为点 的“倒影点”,直线 上有两点 , ,它们的倒影点 , 均在反比例函数 的图象上.若 ,则 .
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式 的解集
(1)探究 的几何意义
如图①,在以 为原点的数轴上,设点 对应的数是 ,由绝对值的定义可知,点 与点 的距离为 ,可记为 .将线段 向右平移1个单位得到线段 ,此时点 对应的数是 ,点 对应的数是1.因为 ,所以 .因此, 的几何意义可以理解为数轴上 所对应的点 与1所对应的点 之间的距离 .
(2)求方程 的解
因为数轴上3和 所对应的点与1所对应的点之间的距离都为2,所以方程的解为3, .
(3)求不等式 的解集
因为 表示数轴上 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数 的范围.
请在图②的数轴上表示 的解集,并写出这个解集.
探究二:探究 的几何意义
(1)探究 的几何意义
如图③,在直角坐标系中,设点 的坐标为 ,过 作 轴于 ,作 轴于 ,则 点坐标为 , 点坐标为 , , ,在 中, ,则 ,因此, 的几何意义可以理解为点 与点 之间的距离 .
(2)探究 的几何意义
如图④,在直角坐标系中,设点 的坐标为 ,由探究二(1)可知, ,将线段 先向右平移1个单位,再向上平移5个单位,得到线段 ,此时点 的坐标为 ,点 的坐标为 ,因为 ,所以 ,因此 的几何意义可以理解为点 与点 之间的距离 .
(3)探究 的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为: .
拓展应用:
(1) 的几何意义可以理解为:点 与点 的距离和点 与点 (填写坐标)的距离之和.
(2) 的最小值为 (直接写出结果)

已知点 , 和直线 ,则点 到直线 的距离证明可用公式 计算.
例如:求点 到直线 的距离.
解:因为直线 ,其中 , .
所以点 到直线 的距离为: .
根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)已知 的圆心 坐标为 ,半径 为2,判断 与直线 的位置关系并说明理由;
(3)已知直线 与 平行,求这两条直线之间的距离.
如图,已知点 、 在反比例函数 的图象上,点 , 在反比例函数 的图象上, , 轴, , 在 轴的两侧, , , 与 间的距离为6,则 的值是 .

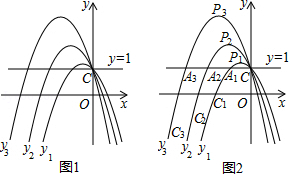
特例感知
(1)如图1,对于抛物线 , , ,下列结论正确的序号是 ;
①抛物线 , , 都经过点 ;
②抛物线 , 的对称轴由抛物线 的对称轴依次向左平移 个单位得到;
③抛物线 , , 与直线 的交点中,相邻两点之间的距离相等.
形成概念
(2)把满足 为正整数)的抛物线称为“系列平移抛物线”.
知识应用
在(2)中,如图2.
①“系列平移抛物线”的顶点依次为 , , , , ,用含 的代数式表示顶点 的坐标,并写出该顶点纵坐标 与横坐标 之间的关系式;
②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”: , , , , ,其横坐标分别为 , , , , 为正整数),判断相邻两点之间的距离是否都相等,若相等,直接写出相邻两点之间的距离;若不相等,说明理由.
③在②中,直线 分别交“系列平移抛物线”于点 , , , , ,连接 , ,判断 , 是否平行?并说明理由.
试题篮
()