电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板上人的质量 之间的函数关系式为 (其中 , 为常数, ,其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻 的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为 ,该读数可以换算为人的质量 ,
温馨提示:①导体两端的电压 ,导体的电阻 ,通过导体的电流 ,满足关系式 ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压

(1)求 , 的值;
(2)求 关于 的函数解析式;
(3)用含 的代数式表示 ;
(4)若电压表量程为 伏,为保护电压表,请确定该电子体重秤可称的最大质量.
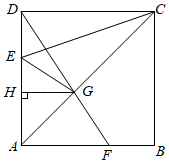
如图,点 在正方形 边 上,点 是线段 上的动点(不与点 重合), 交 于点 , 于点 , , .
(1)求 ;
(2)设 , ,试探究 与 的函数关系式(写出 的取值范围);
(3)当 时,判断 与 的位置关系并说明理由.
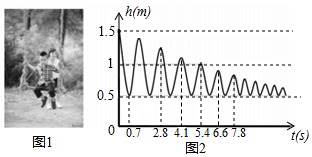
小红帮弟弟荡秋千(如图 ,秋千离地面的高度 与摆动时间 之间的关系如图2所示.
(1)根据函数的定义,请判断变量 是否为关于 的函数?
(2)结合图象回答:
①当 时, 的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多少时间?
某个函数具有性质:当 时, 随 的增大而增大,这个函数的表达式可以是 (只要写出一个符合题意的答案即可).
如图,四边形 为一个矩形纸片, , ,动点 自 点出发沿 方向运动至 点后停止, 以直线 为轴翻折,点 落在点 的位置.设 ,△ 与原纸片重叠部分的面积为 .

(1)当 为何值时,直线 过点 ?
(2)当 为何值时,直线 过 的中点 ?
(3)求出 与 的函数表达式.
同一温度的华氏度数 与摄氏度数 之间的函数表达式是 .若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 .
已知某厂以 小时 千克的速度匀速生产某种产品(生产条件要求 ,且每小时可获得利润 元.
(1)某人将每小时获得的利润设为 元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行解析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
如图,在矩形 中, , ,点 为边 上的一点(与 、 不重合),四边形 关于直线 的对称图形为四边形 ,延长 交 于点 ,记四边形 的面积为 .
(1)若 ,求 的值;
(2)设 ,求 关于 的函数表达式.

【了解概念】
有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.

【理解运用】
(1)如图①,对余四边形 中, , , ,连接 .若 ,求 的值;
(2)如图②,凸四边形 中, , ,当 时,判断四边形 是否为对余四边形.证明你的结论;
【拓展提升】
(3)在平面直角坐标系中,点 , , ,四边形 是对余四边形,点 在对余线 上,且位于 内部, .设 ,点 的纵坐标为 ,请直接写出 关于 的函数解析式.
阅读下面的材料:
如果函数 满足:对于自变量 的取值范围内的任意 , ,
(1)若 ,都有 ,则称 是增函数;
(2)若 ,都有 ,则称 是减函数.
例题:证明函数 是减函数.
证明:设 ,
.
,
, .
.即 .
.
函数 是减函数.
根据以上材料,解答下面的问题:
已知函数 ,
,
(1)计算: , ;
(2)猜想:函数 是 函数(填“增”或“减” ;
(3)请仿照例题证明你的猜想.
试题篮
()