初中数学方差试题

"惜餐为荣，殄物为耻"，为了解落实"光盘行动"的情况，某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量．从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据（单位： $\mathit{kg})$ ，进行整理和分析（餐厨垃圾质量用 $x$ 表示，共分为四个等级： $A$ ． $x<1$ ， $B.1⩽x<1.5$ ， $C.1.5⩽x<2$ ， $D$ ． $x⩾2)$ ，下面给出了部分信息．

七年级10个班的餐厨垃圾质量：0.8，0.8，0.8，0.9，1.1，1.1，1.6，1.7，1.9，2.3．

八年级10个班的餐厨垃圾质量中 $B$ 等级包含的所有数据为：1.0，1.0，1.0，1.0，1.2．

七、八年级抽取的班级餐厨垃圾质量统计表

年级	平均数	中位数	众数	方差	$A$ 等级所占百分比
七年级	1.3	1.1	$a$	0.26	$40\%$
八年级	1.3	$b$	1.0	0.23	$m\%$

根据以上信息，解答下列问题：

（1）直接写出上述表中 $a$ ， $b$ ， $m$ 的值；

（2）该校八年级共30个班，估计八年级这一天餐厨垃圾质量符合 $A$ 等级的班级数；

（3）根据以上数据，你认为该校七、八年级的"光盘行动"，哪个年级落实得更好？请说明理由（写出一条理由即可）．

超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋，设货架上原有鸡蛋的质量（单位： $g)$ 平均数和方差分别为 $\bar{x}$ ， $s^2$ ，该顾客选购的鸡蛋的质量平均数和方差分别为 $\overline{x_1}$ ， $s_1^2$ ，则下列结论一定成立的是 $($ 　　 $)$

A．

$\bar{x}<\overline{x_1}$

B．

$\bar{x}>\overline{x_1}$

C．

$s^2>s_1^2$

D．

$s^2<s_1^2$

甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 $\bar{x}$ （单位：环）及方差 $S^2$ （单位：环 ${}^2)$ 如下表所示：

	甲	乙	丙	丁
$\bar{x}$	9	8	9	9
$S^2$	1.6	0.8	3	0.8

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择 $($ 　　 $)$

A．

甲

B．

乙

C．

丙

D．

丁

小聪、小明准备代表班级参加学校"党史知识"竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：

（1）要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．

（2）求小聪成绩的方差．

（3）现求得小明成绩的方差为 $S_{\mathit{小明}}^2=3$ （单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．

从甲、乙、丙三人中选一人参加环保知识决赛，经过两轮测试，他们的平均成绩都是88.9，方差分别是 $S_{甲}^2=2.25$， $S_{乙}^2=1.81$， $S_{丙}^2=3.42$，你认为最适合参加决赛的选手是 　　（填“甲”或“乙”或“丙” $)$．

下列说法正确的是 $($ 　　 $)$

A．	一个不透明的口袋中有3个白球和2个红球（每个球除颜色外都相同），则从中任意摸出一个球是红球的概率为 $\frac{2}{3}$
B．	一个抽奖活动的中奖概率为 $\frac{1}{2}$ ，则抽奖2次就必有1次中奖
C．	统计甲，乙两名同学在若干次检测中的数学成绩发现： $\overline{x_{甲}}=\overline{x_{乙}}$ ， $S_{甲}^2>S_{乙}^2$ ，说明甲的数学成绩比乙的数学成绩稳定
D．	要了解一个班有多少同学知道"杂交水稻之父"袁隆平的事迹，宜采用普查的调查方式

据统计，某班7个学习小组上周参加"青年大学习"的人数分别为：5，5，6，6，6，7，7．下列说法错误的是 $($ 　　 $)$

A．	该组数据的中位数是6	B．	该组数据的众数是6
C．	该组数据的平均数是6	D．	该组数据的方差是6

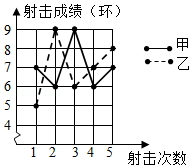
如图是根据甲、乙两人5次射击的成绩（环数）制作的折线统计图．你认为谁的成绩较为稳定？ 　　（填"甲"或"乙" $)$

一组数据：1，2，2，3，若添加一个数据3，则不发生变化的统计量是 $($ 　　 $)$

A．

平均数

B．

中位数

C．

众数

D．

方差

下列说法正确的是（　　）

A．	为了了解全国中学生的心理健康情况，选择全面调查
B．	在一组数据7，6，5，6，6，4，8中，众数和中位数都是6
C．	"若a是实数，则 $\left|a\right|＞0$ "是必然事件
D．	若甲组数据的方差 $S_{甲}{}^2＝0.02$ ，乙组数据的方差 $S_{乙}{}^2＝0.12$ ，则乙组数据比甲组数据稳定

为调动学生参与体育锻炼的积极性，某校组织了一分钟跳绳比赛活动，体育组随机抽取了10名参赛学生的成绩，将这组数据整理后制成统计表：

一分钟跳绳个数（个     $)$	141	144	145	146
学生人数（名     $)$	5	2	1	2

则关于这组数据的结论正确的是 $($ 　　 $)$

A．	平均数是144	B．	众数是141
C．	中位数是144.5	D．	方差是5.4

2021年是中国共产党成立100周年．为普及党史知识，培养爱国主义精神，今年五月份，某市党校举行党史知识竞赛，每个班级各选派15名学员参加了网上测试，现对甲、乙两班学员的分数进行整理分析如下：

甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98．

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89

（1）按如表分数段整理两班测试成绩

班级	$70.5~75.5$	$75.5~80.5$	$80.5~85.5$	$85.5~90.5$	$90.5~95.5$	$95.5~100.5$
甲	1	2	$a$	5	1	2
乙	0	3	3	6	2	1

表中 $a=$　　；

（2）补全甲班15名学员测试成绩的频数分布直方图；

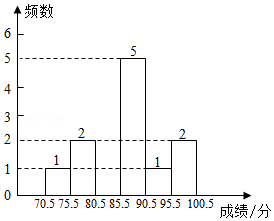
（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

班级	平均数	众数	中位数	方差
甲	86	$x$	86	44.8
乙	86	88	$y$	36.7

表中 $x=$　　， $y=$　　．

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是 　　班；

（5）本次测试两班的最高分都是98分，其中甲班2人，乙班1人．现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，根据树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率．

在2021年初中毕业生体育测试中，某校随机抽取了10名男生的引体向上成绩，将这组数据整理后制成如下统计表：

成绩（次 $)$	12	11	10	9
人数（名 $)$	1	3	4	2

关于这组数据的结论不正确的是 $($ 　　 $)$

A．

中位数是10.5

B．

平均数是10.3

C．

众数是10

D．

方差是0.81

某人5次射击命中的环数分别为5，10，7， $x$，10．若这组数据的中位数为8，则这组数据的方差为 　　．

某人5次射击命中的环数分别为5，10，7， $x$，10．若这组数据的中位数为8，则这组数据的方差为 　　．