已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.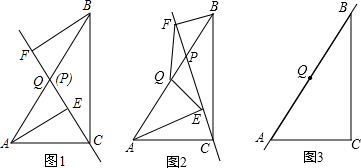
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)折叠后,DC的对应线段是 ,CF的对应线段是 ;
(2)△EBF是等腰三角形吗?请说明理由;
(3)若AB=4,AD=8,求△EBF的面积.
在下列各组条件中,不能说明△ABC≌△DEF的是()
| A.AB=DE,∠B=∠E,∠C=∠F |
| B.AC=DF,BC=EF,∠A=∠D |
| C.AB=DE,∠A=∠D,∠B=∠E |
| D.AB=DE,BC=EF,AC=DF |
下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是()
A.2cm,4cm, cm cm |
B.1cm,1cm,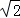 cm cm |
C.1cm,2cm,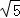 cm cm |
D.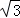 cm,2cm, cm,2cm,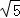 cm cm |
如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
如图,△ABC是等边三角形,点D、E分别是BC、CA的延长线上的点,且CD=AE,DA的延长线交BE于点F.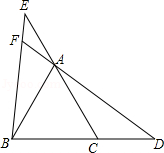
(1)求证:AD=BE;
(2)求∠BFD的度数.
如图,已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,且D、E、C三点在一直线上.若AD=AE=1,DE=2EC,则BC= .
试题篮
()