(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.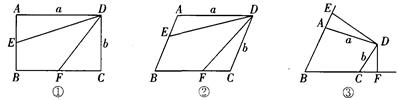
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.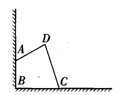
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号