将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。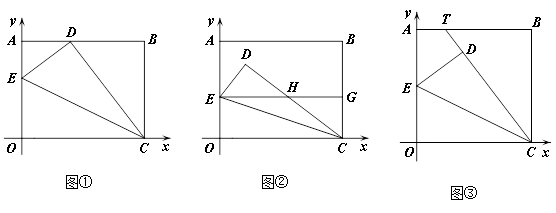
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号