在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图①,然后拼成一个梯形,如图②,根据这两个图形的面积关系,表明下列式子成立的是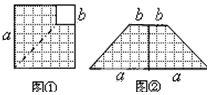
| A.a2-b2=(a+b)(a-b) | B.(a+b)2=a2+2ab+b2 |
| C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)2 |
相关知识点
推荐试卷
在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图①,然后拼成一个梯形,如图②,根据这两个图形的面积关系,表明下列式子成立的是
| A.a2-b2=(a+b)(a-b) | B.(a+b)2=a2+2ab+b2 |
| C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)2 |
试题篮
()