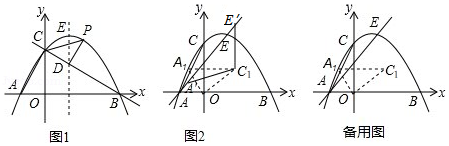
如图1,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 ,抛物线的顶点为点 .
(1)判断 的形状,并说明理由;
(2)经过 , 两点的直线交抛物线的对称轴于点 ,点 为直线 上方抛物线上的一动点,当 的面积最大时, 从点 出发,先沿适当的路径运动到抛物线的对称轴上点 处,再沿垂直于抛物线对称轴的方向运动到 轴上的点 处,最后沿适当的路径运动到点 处停止.当点 的运动路径最短时,求点 的坐标及点 经过的最短路径的长;
(3)如图2,平移抛物线,使抛物线的顶点 在射线 上移动,点 平移后的对应点为点 ,点 的对应点为点 ,将 绕点 顺时针旋转至△ 的位置,点 , 的对应点分别为点 , ,且点 恰好落在 上,连接 , ,△ 是否能为等腰三角形?若能,请求出所有符合条件的点 的坐标;若不能,请说明理由.
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号