如图,在中,,以为直径的交于点,连接,过点作,垂足为,、的延长线交于点.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
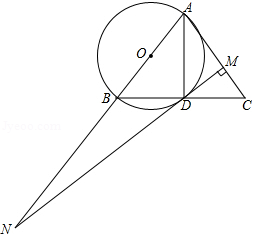
证明:(1)如图,连接,
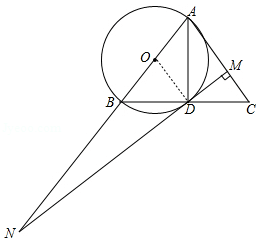
是直径,
,
又,
,,
,,
,
,
,
又是半径,
是的切线;
(2),
,
,,
,
,
,
又,
,
,
;
(3),,
,
,
,
,
,
,
,
,,
,
,
,
.
相关知识点
推荐试卷
如图,在中,,以为直径的交于点,连接,过点作,垂足为,、的延长线交于点.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.

证明:(1)如图,连接,

是直径,
,
又,
,,
,,
,
,
,
又是半径,
是的切线;
(2),
,
,,
,
,
,
又,
,
,
;
(3),,
,
,
,
,
,
,
,
,,
,
,
,
.
试题篮
()