如图,矩形OABC的两边OA,OC分别在x轴和y轴的正半轴上,点B的坐标为( ),点D在CB上,且CD:DB=2:1,OB交AD于点E.平行于x轴的直线l从原点O出发,以每秒1个单位长度的速度沿y轴向上平移,到C点时停止;l与线段OB,AD分别相交与M,N两点,以MN为边作等边△MNP(点P在线段MN的下方).设直线l的运动时间为t(秒),△MNP与△OAB重叠部分的面积为S(平分单位).
(1)直接写出点E的坐标;
(2)求S与t的函数关系式;
(3)是否存在某一时刻t,使得 成立?若存在,请求出此时t的值;若不存在,请说明理由.
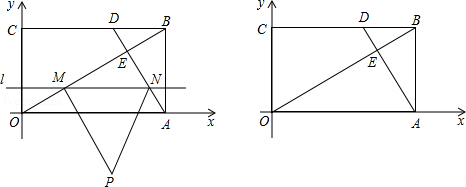
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号