阅读下面材料,完成(1) (3)题
数学课上,老师出示了这样一道题:如图1, 中, ,点 、 在 上, , (其中 , 的平分线与 相交于点 , ,垂足为 ,探究线段 与 的数量关系,并证明.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现 与 相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段 与 的数量关系.”
老师:“保留原题条件,延长图1中的 ,与 相交于点 (如图 ,可以求出 的值.”
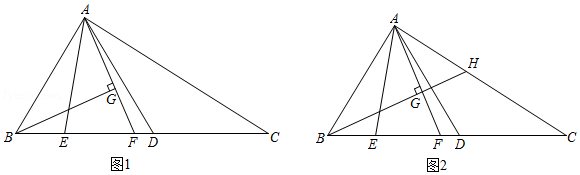
(1)求证: ;
(2)探究线段 与 的数量关系(用含 的代数式表示),并证明;
(3)直接写出 的值(用含 的代数式表示).
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号