在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程 ,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点 , ;
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点 ,另一条直角边恒过点 ;
第三步:在移动过程中,当三角板的直角顶点落在 轴上点 处时,点 的横坐标 即为该方程的一个实数根(如图 ;
第四步:调整三角板直角顶点的位置,当它落在 轴上另一点 处时,点 的横坐标 即为该方程的另一个实数根.
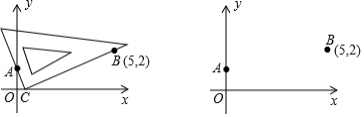
(1)在图2中,按照“第四步”的操作方法作出点 (请保留作出点 时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的 就是方程 的一个实数根;
(3)上述操作的关键是确定两个固定点的位置.若要以此方法找到一元二次方程 的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 , , , 与 , , 之间满足怎样的关系时,点 , , , 就是符合要求的一对固定点?
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号