把正整数按照下面的表格进行排列
| 1 |
3 |
6 |
10 |
15 |
21 |
…… |
| 2 |
5 |
9 |
14 |
20 |
…… |
…… |
| 4 |
8 |
13 |
19 |
…… |
…… |
…… |
| 7 |
12 |
18 |
…… |
…… |
…… |
…… |
| 11 |
17 |
…… |
…… |
…… |
…… |
…… |
| 16 |
…… |
…… |
…… |
…… |
…… |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
则排在第6行,第4列的数是_______________;
排在第 行,第
行,第 列(
列( )的数是______________
)的数是______________
下表给出了一个“三角形数阵”:
依照表中数的分布规律,可猜得第10行第6个数是
已知大于1的任意一个自然数的三次幂都可表示成连续奇数的和.如:
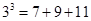

若 是自然数,把
是自然数,把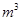 按上述表示,等式右侧的奇数中含有2015,则
按上述表示,等式右侧的奇数中含有2015,则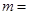 .
.
试题篮
()