已知数列{an}的前n项和Sn,a1=﹣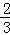 ,Sn+
,Sn+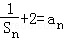 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=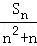 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣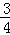 .
.
(本小题满分14分)设数列 的前
的前 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,
(1)求数列 的前三项
的前三项 ;
;
(2)猜想数列 的通项公式
的通项公式 ,并用数学归纳法证明;
,并用数学归纳法证明; (3)求证:对任意
(3)求证:对任意 都有
都有 .
.
(本小题满分12分)
给出四个等式: ;
; ;
; ;
;

 .猜测第
.猜测第 个等式,并用数学归纳法证明.
个等式,并用数学归纳法证明.
已知数列 满足
满足 ,
,
(1)求 ,
, ,
, ,
, ;
;
(2)归纳猜想出通项公式 ,并且用数学归纳法证明;
,并且用数学归纳法证明;
(3)求证 能被15整除.
能被15整除.
已知 .经计算得
.经计算得
 .
.
(Ⅰ)由上面数据,试猜想出一个一般性结论;
(Ⅱ)用数学归纳法证明你的猜想.
(本小题满分14分)若 为正整数,试比较
为正整数,试比较 与
与 的大小,分别取
的大小,分别取 加以试验,根据试验结果猜测一个一般性结论,并用数学归纳法证明.
加以试验,根据试验结果猜测一个一般性结论,并用数学归纳法证明.
试题篮
()