高中数学第二数学归纳法解答题

已知数列中，，且．为数列的前项和，且．
（1）求数列的通项公式；
（2）设，求数列的前项的和；
（3）证明对一切，有．

设数列{}满足：a₁=2，对一切正整数n，都有
(1)探讨数列{}是否为等比数列，并说明理由；
(2)设

已知数列{b_n}是等差数列，b₁＝1，b₁＋b₂＋…＋b₁₀＝145.
(1)求数列{b_n}的通项公式b_n；
(2)设数列{a_n}的通项a_n＝log_a(其中a＞0且a≠1)．记S_n是数列{a_n}的前n项和，试比较S_n与log_ab_n＋1的大小，并证明你的结论.

各项均为正数的数列对一切均满足．证明：
（1）；
（2）．

已知，是函数的两个零点，其中常数，，设．
（Ⅰ）用，表示，；
（Ⅱ）求证：；
（Ⅲ）求证：对任意的．

记的展开式中，的系数为，的系数为,其中
(1)求（2）是否存在常数p,q(p<q),使，对，恒成立？证明你的结论.

是否存在常数a,b使等式对于一切n∈N*都成立？若存在，求出a,b的值，若不存在，请说明理由。

已知，，．
（1）当时，试比较与的大小关系；
（2）猜想与的大小关系，并给出证明．

若不等式＋＋…＋>对一切正整数n都成立，猜想正整数a的最大值，并证明结论．

（本小题满分10分）
如图：假设三角形数表中的第n+1行的第二个数为（n≥1，n∈N^*）

（1）归纳出与的关系式, 并求出的通项公式；
（2）设，求证： 

已知数列的各项均为正整数，对于任意n∈N^*，都有 成立，且．
（1）求，的值；
（2）猜想数列的通项公式，并给出证明．

【原创】
（1）观察下列各式;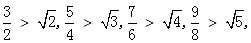根据以上各式利用归纳推理得出一个一般性的结论；
（2）设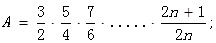根据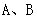的大小关系证明（1）的结论；

（本小题满分12分）设令.
（Ⅰ）求的值；
（Ⅱ）猜想数列的通项公式，并用数学归纳法证明.

用数学归纳法证明等式时，写出到时左边应增加的项为？

已知为等差数列，且，公差.
（1）数列满足结论；；试证：；
（2）根据（1）中的几个等式，试归纳出更一般的结论，并用数学归纳法证明.