已知 ,
, ,
, .
.
(1)当 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
在数列 中,已知
中,已知 ,
, ,
, (
( ,
, ).
).
(1)当 ,
, 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数 ,使得
,使得 为完全平方数.
为完全平方数.
已知数列 中,
中, ,
, 且
且
 .
. 为数列
为数列 的前
的前 项和,且
项和,且
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项的和
项的和 ;
;
(3)证明对一切 ,有
,有 .
.
(本小题满分13分)已知数列 中,
中,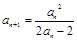 ,
,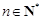 .
.
(Ⅰ)若 ,设
,设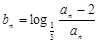 ,求证数列
,求证数列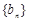 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
,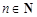 ,证明:
,证明: .
.
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1)函数f(x)在区间(0,1)是增函数;
(2)an<an+1<1.
试题篮
()