高中物理放射性同位素的应用试题

如图所示，A、B两物体相距s=7m，物体A以v_A=4m/s的速度向右匀速运动。而物体B此时的速度v_B=10m/s，向右做匀减速运动，加速度a =－2m/s²。那么物体A追上物体B所用的时间为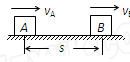

A．7s        B．8s       C．9s       D．10s

一质点以某初速度沿足够长的光滑斜面向上滑动，其运动情况经仪器监控扫描，输入计算机后得到该运动质点位移方程为x＝12t－2t²(m)．则该质点在时间t从0～4 s内经过的路程为

A．16 m

B．18 m

C．20 m

D．22 m

物体从静止开始做匀加速直线运动,在第2秒内的位移为s米，则物体运动的加速度大小是

A．m/s^2

B．m/s^2

C．m/s^2

D．m/s^2

物体的初速度为v₀，以加速度a做匀加速直线运动，如果要它的速度增加到初速度的n倍，则物体的位移是

A．

B．

C．

D．

质量为m=1kg的物体以初速V₀=12m/s竖直上抛，空气阻力大小为其重力的0.2倍，g取10m/s²，求：
（1）该物体上升和下降时的加速度之比；
（2）求整个过程中物体克服阻力做功的平均功率P₁和物体落回抛出点时重力的瞬时功率P₂。

为确保弯道行车安全，汽车进入弯道前必须减速．如图所示，AB为进入弯道前的平直公路，BC为水平圆弧形弯道．已知AB段的距离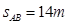，弯道半径R=24m．汽车到达A点时速度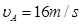，汽车与路面间的动摩擦因数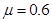，设最大静摩擦力等于滑动摩擦力，取g=l0m／s²．要确保汽车进入弯道后不侧滑．求汽车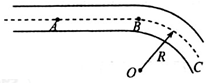

(1)在弯道上行驶的最大速度；
(2)在AB段做匀减速运动的最小加速度．

在德国首都柏林举行的世界田径锦标赛女子跳高决赛中，克罗地亚选手弗拉希奇以2.04m的成绩获得冠军。弗拉希奇身高约为1.93 m，忽略空气阻力，g取10 m/s²。则下列说法正确的是

A．弗拉希奇下降过程处于失重状态

B．弗拉希奇起跳以后在上升过程处于超重状态

C．弗拉希奇起跳时地面对她的支持力大于她所受的重力

D．弗拉希奇起跳离开地面时的初速度大约为3 m/s

如图所示,电梯质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动.当上升高度为H时,电梯的速度达到v,则在这段过程中,下列说法中正确的是(    )

A．电梯地板对物体的支持力所做的功等于

B．电梯地板对物体的支持力所做的功大于

C．钢索的拉力所做的功等于

D．钢索的拉力所做的功大于

如图所示，一块涂有炭黑的玻璃板，质量为2kg，在拉力F的作用下，由静止开始竖直向上做匀加速直线运动。一个装有水平振针的振动频率为5 Hz的固定电动音叉（其振幅可以变化，但频率保持不变）在玻璃板上画出了图示曲线，量得OA="1" cm，OB="4" cm，OC="9" cm。则拉力F的大小为（   ）（不计一切摩擦，g取10 m/s²）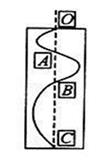

A．4N

B．24N

C．1N

D．21N

如图所示为某汽车在平直公路上启动时发动机功率P随时间t变化的图象，P₀为发动机的额定功率。已知在t₂时刻汽车的速度已经达到最大v_m，汽车受到的空气阻力与地面摩擦力之和随速度增大而增大。由此可得

A．在0~t1时间内，汽车一定做匀加速度运动

B．在t1~t2时间内，汽车一定做匀速运动

C．在t2~t3时间内，汽车一定做匀速运动

D．在t3时刻，汽车速度一定等于vm

某汽车训练场地有如图设计，在平直的道路上，依次有编号为A、B、C、D、E的五根标志杆，相邻杆之间的距离ΔL＝12.0 m。一次训练中，学员驾驶汽车以57.6km/h的速度匀速向标志杆驶来，教练与学员坐在同排观察并记录时间。当教练经过O点时向学员发出指令：“立即刹车”，同时用秒表开始计时。忽略反应时间，刹车后汽车做匀减速直线运动，停在D标杆附近。教练记录自己经过C杆时秒表的读数为t_C＝6.0 s，已知L_OA＝36m，教练距车头的距离Δs＝1.5 m。求：

(1)刹车后汽车做匀减速运动的加速度大小a；
(2)汽车停止运动时，车头离标志杆D的距离Δx。

一足够大的倾角为45º的斜面上有一点O，O点正上方h=0.4m处有一点P。在P点以水平速度v₀=1m/s抛出一个小球，随着抛出方向的不同，小球将落到斜面上的不同位置。不计空气阻力，重力加速度g取10m/s²。试求小球落到斜面上的位置距离O点的最大值和最小值。

如图所示，AKD为竖直平面内固定的光滑绝缘轨道，轨道间均平滑连接，AK段水平，其间分布有一水平向右的匀强电场I。PQ为同一竖直面内的固定光滑水平轨道。自D点向右宽度L=0.7m的空间，分布有水平向右、场强大小E=1.4×10⁵N/C的匀强电场II。质量m₂=0.1kg、长度也为L的不带电绝缘平板，静止在PQ上并恰好处于电场II中，板的上表面与弧形轨道相切于D点。AK轨道上一带正电的小物体从电场I的左边界由静止开始运动，并在D点以速度v=1m/s滑上平板。已知小物体的质量m₁=10^－2kg，电荷量q=＋10^－7C,与平板间的动摩擦因数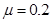,AK与D点的垂直距离为h=0.3m，小物体离开电场II时速度比平板的大、小物体始终在平板上。设小物体电荷量保持不变且视为质点，取g=10m/s²。求：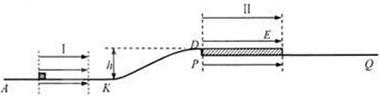

（1）电场I左右边界的电势差；
（2）小物体从离开电场II开始，到平板速度最大时，所需要的时间。

如图所示，水平平台ab长为20m，平台b端与长度未知的特殊材料制成的斜面bc连接，斜面倾角为30°.在平台b端放上质量为5kg的物块，并给物块施加与水平方向成37°角的50N推力后，物块由静止开始运动．己知物块与平台间的动摩擦因数为0.4，重力加速度g=10m/s²，sin37°=0.6，求：(第(2)、(3)两问结果保留三位有效数字)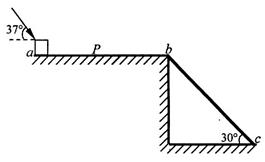

(1)物块由a运动到b所用的时间；
(2)若物块从a端运动到P点时撤掉推力，则物块刚好能从斜面b端开始下滑，则间aP的距离为多少?(物块在b端无能量损失)
(3)若物块与斜面间的动摩擦因数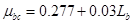，式中L_b为物块在斜面上所处的位置离b端的距离，在(2)中的情况下，物块沿斜面滑到什么位置时速度最大?

如图所示，光滑水平面上有一矩形长木板，木板左端放一小物块，已知木板质量大于物块质量，t=0时两者从图中位置以相同的水平速度v₀向右运动，碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来，运动过程中物块一直未离开木板，则关于物块运动的速度v随时间t变化的图象可能正确的是