为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该户居民5、6两个月共交水费多少元.
在实数的原有运算法则中我们补充定义新运算“⊕”如下:当a≥b时,a⊕b=b2;当a<b时,a⊕b=a.则当x=2时,(1⊕x)-(3⊕x)的值为 .
仔细观察下列三组数:
第一组:1,4,9,16,25,…
第二组:1,8,27,64,125,…
第三组:﹣2,﹣8,﹣18,﹣32,﹣50,…
(1)写出每组的第6个数各是多少?
(2)第二组的第100个数是第一组的第100个数的多少倍?
(3)取每组数的第n个数,计算这三个数的和.
某一食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
这批样品的平均质量比标准质量多还是少?多或少几克,若标准质量为450克,则抽样检测的总质量是多少?
有一批水果,包装质量为每筐25千克,现抽取10筐样品进行检测,结果称重如下(单位:千克):21,24,27,28,25,26,22,23,25,26为了求得10筐样品的总质量,我们可以选取一个恰当的基准数进行简化运算.
| 原质量 |
21 |
24 |
27 |
28 |
25 |
26 |
22 |
23 |
25 |
26 |
| 与基准数的差距 |
|
|
|
|
|
|
|
|
|
|
(1)你认为选取的一个恰当的基准数为____________;
(2)根据你选取的基准数,用正、负数填写上表;
(3)这10筐水果的总质量是多少千克?
已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=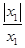 ,则
,则 = ;
= ;
(2)若y2= ,则
,则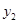 = ;
= ;
(3)若y3=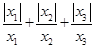 ,则
,则 = ;
= ;
(4)由以上探究可知,y2012= ,
,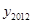 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
下图是一个数字转换机,请解答下列问题:

(1)填空:若输入的x值为2,则输出的y值为
(2)若输入的x值为1,则输出的y值为
(3)若输出的y值为28,那么输入的x值是什么?(写出三个x值,并写出简要的分析过程.)
有20筐白菜,以每筐25千克为标准,超过千克数记为正数,不足的千克数记为负数,记录如表:
| 与标准质量的差值(单位:千克) |
-3 |
-2 |
-1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
4 |
6 |
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
计算:
(1)(-3)+(+9)
(2)-20+(+3)-(-5)-(+7)
(3)(-7)×(-5)-90÷(-15)
(4)-102+[(-4)2+(3+32)×2]÷(-2)3.
试题篮
()