快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了 ;
②快车速度比慢车速度多 ;
③图中 ;
④快车先到达目的地.
其中正确的是

| A. |
①③ |
B. |
②③ |
C. |
②④ |
D. |
①④ |
甲、乙两地的路程为290千米,一辆汽车早上从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进,当离甲地路程为240千米时接到通知,要求中午
准时到达乙地.设汽车出发
小时后离甲地的路程为
千米,图中折线
表示接到通知前
与
之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为 千米小时;
(2)求线段所表示的
与
之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.

某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元.

某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.
(1)设该商店购进甲型平板电脑 台,请写出全部售出后该商店获利 与 之间函数表达式.
(2)若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.
某电商积极响应市政府号召,在线销售甲、乙、丙三种农产品,已知 乙产品的售价比 甲产品的售价多5元, 丙产品的售价是 甲产品售价的3倍,用270元购买丙产品的数量是用60元购买乙产品数量的3倍.
(1)求甲、乙、丙三种农产品每千克的售价分别是多少元?
(2)电商推出如下销售方案:甲、乙、丙三种农产品搭配销售共 ,其中乙产品的数量是丙产品数量的2倍,且甲、丙两种产品数量之和不超过乙产品数量的3倍.请你帮忙计算,按此方案购买 农产品最少要花费多少元?
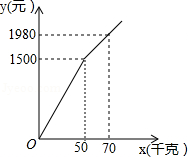
受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售."一方有难,八方支援"某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元 千克的价格出售.设经销商购进甲种水果 千克,付款 元, 与 之间的函数关系如图所示.
(1)直接写出当 和 时, 与 之间的函数关系式;
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额 (元 最少?
(3)若甲,乙两种水果的销售价格分别为40元 千克和36元 千克.经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共 千克,且销售完 千克水果获得的利润不少于1650元,求 的最小值.
5月18日,我市九年级学生安全有序开学复课.为切实做好疫情防控工作,开学前夕,我市某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.
(1)求每盒口罩和每盒水银体温计的价格各是多少元?
(2)如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩 盒 为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含 的代数式表示.
(3)在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付 元,求 关于 的函数关系式.若该校九年级有900名学生,需要购买口罩和水银体温计各多少盒?所需总费用为多少元?
小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为 (分钟),图1表示两人之间的距离 (米 与时间 (分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米 与时间 (分钟)的函数关系的图象的一部分,请根据所给信息答案下列问题:
(1)填空:妈妈骑车的速度是 米 分钟,妈妈在家装载货物所用时间是 分钟,点 的坐标是 .
(2)直接写出妈妈和商店的距离 (米 与时间 (分钟)的函数关系式,并在图2中画出其函数图象;
(3)求 为何值时,两人相距360米.

某公司分别在 , 两城生产同种产品,共100件. 城生产产品的总成本 (万元)与产品数量 (件 之间具有函数关系 .当 时, ;当 时, . 城生产产品的每件成本为70万元.
(1)求 , 的值;
(2)当 , 两城生产这批产品的总成本的和最少时,求 , 两城各生产多少件?
(3)从 城把该产品运往 , 两地的费用分别为 万元 件和3万元 件;从 城把该产品运往 , 两地的费用分别为1万元 件和2万元 件. 地需要90件, 地需要10件,在(2)的条件下,直接写出 , 两城总运费的和的最小值(用含有 的式子表示).
一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始 内只进水不出水,从第 到第 内既进水又出水,从第 开始只出水不进水,容器内水量 (单位: 与时间 (单位: 之间的关系如图所示,则图中 的值是

| A. |
32 |
B. |
34 |
C. |
36 |
D. |
38 |
某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元 台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第 天 为整数)的生产成本为 (元 台), 与 的关系如图所示.
(1)若第 天可以生产这种设备 台,则 与 的函数关系式为 , 的取值范围为 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.

为了抗击新冠疫情,我市甲、乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨.这批防疫物资将运往 地240吨, 地260吨,运费如下表(单位:元 吨).
| 目的地 生产厂 |
|
|
| 甲 |
20 |
25 |
| 乙 |
15 |
24 |
(1)求甲、乙两厂各生产了这批防疫物资多少吨?
(2)设这批物资从乙厂运往 地 吨,全部运往 , 两地的总运费为 元.求 与 之间的函数关系式,并设计使总运费最少的调运方案;
(3)当每吨运费均降低 元 且 为整数)时,按(2)中设计的调运方案运输,总运费不超过5200元.求 的最小值.
2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第 天 为正整数)的销售价格 (元 千克)关于 的函数关系式为 ,销售量 (千克)与 之间的关系如图所示.
(1)求 与 之间的函数关系式,并写出 的取值范围;
(2)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额 销售量 销售价格)

某校足球队需购买 、 两种品牌的足球.已知 品牌足球的单价比 品牌足球的单价高20元,且用900元购买 品牌足球的数量用720元购买 品牌足球的数量相等.
(1)求 、 两种品牌足球的单价;
(2)若足球队计划购买 、 两种品牌的足球共90个,且 品牌足球的数量不小于 品牌足球数量的2倍,购买两种品牌足球的总费用不超过8500元.设购买 品牌足球 个,总费用为 元,则该队共有几种购买方案?采用哪一种购买方案可使总费用最低?最低费用是多少元?
试题篮
()