初中数学一次函数的应用试题

如图是王阿姨晚饭后步行的路程 $S$（单位： $m)$与时间 $t$（单位： $\mathit{min})$的函数图象，其中曲线段 $\mathit{AB}$是以 $B$为顶点的抛物线一部分．下列说法不正确的是 $($　　 $)$

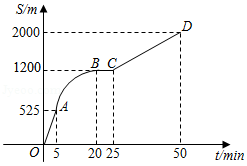
A． $25\mathit{min}~50\mathit{min}$，王阿姨步行的路程为 $800m$

B．线段 $\mathit{CD}$的函数解析式为 $S=32t+400(25⩽t⩽50)$

C． $5\mathit{min}~20\mathit{min}$，王阿姨步行速度由慢到快

D．曲线段 $\mathit{AB}$的函数解析式为 $S=-3{(t-20)}^2+1200(5⩽t⩽20)$

某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品 $x$（吨），生产甲、乙两种产品获得的总利润为 $y$（万元）．

（1）求 $y$与 $x$之间的函数表达式；

（2）若每生产1吨甲产品需要 $A$原料0.25吨，每生产1吨乙产品需要 $A$原料0.5吨．受市场影响，该厂能获得的 $A$原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为 $x$小时，快车行驶的路程为 $y_1$千米，慢车行驶的路程为 $y_2$千米．如图中折线 $\mathit{OAEC}$表示 $y_1$与 $x$之间的函数关系，线段 $\mathit{OD}$表示 $y_2$与 $x$之间的函数关系．

请解答下列问题：

（1）求快车和慢车的速度；

（2）求图中线段 $\mathit{EC}$所表示的 $y_1$与 $x$之间的函数表达式；

（3）线段 $\mathit{OD}$与线段 $\mathit{EC}$相交于点 $F$，直接写出点 $F$的坐标，并解释点 $F$的实际意义．

某水果店以每千克8元的价格购进苹果若干千克，销售了部分苹果后，余下的苹果每千克降价4元销售，全部售完．销售金额 $y$（元 $)$与销售量 $x$（千克）之间的关系如图所示，请根据图象提供的信息完成下列问题：

（1）降价前苹果的销售单价是　     　元 $/$千克；

（2）求降价后销售金额 $y$（元 $)$与销售量 $x$（千克）之间的函数解析式，并写出自变量的取值范围；

（3）该水果店这次销售苹果盈利了多少元？

一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地，两车之间的距离 $y$（千米）与行驶时间 $x$（小时）的对应关系如图所示：

（1）甲乙两地相距多远？

（2）求快车和慢车的速度分别是多少？

（3）求出两车相遇后 $y$与 $x$之间的函数关系式；

（4）何时两车相距300千米．

某周日上午 $8:00$小宇从家出发，乘车1小时到达某活动中心参加实践活动． $11:00$时他在活动中心接到爸爸的电话，因急事要求他在 $12:00$前回到家，他即刻按照来活动中心时的路线，以5千米 $/$小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 $x$（小时）后，到达离家 $y$（千米）的地方，图中折线 $\mathit{OABCD}$表示 $y$与 $x$之间的函数关系．

（1）活动中心与小宇家相距　   　千米，小宇在活动中心活动时间为　 　小时，他从活动中心返家时，步行用了　    　小时；

（2）求线段 $\mathit{BC}$所表示的 $y$（千米）与 $x$（小时）之间的函数关系式（不必写出 $x$所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在 $12:00$前回到家，并说明理由．

小强的爸爸从家骑自行车去图书馆借书，途中遇到了从图书馆步行回家的小强，爸爸借完书后迅速回家，途中追上了小强，便用自行车载上小强一起回家，结果爸爸比自己单独骑车回家晚到1分钟，两人与家的距离 $S$（千米）和爸爸从家出发后的时间 $t$（分钟）之间的关系如图所示．

（1）图书馆离家有多少千米？

（2）爸爸和小强第一次相遇时，离家多少千米？

（3）爸爸载上小强后一起回家的速度是多少？

暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离 $y\left(\mathit{km}\right)$与汽车行驶时间 $x\left(h\right)$之间的函数图象如图所示．

（1）从小刚家到该景区乘车一共用了多少时间？

（2）求线段 $\mathit{AB}$对应的函数解析式；

（3）小刚一家出发2.5小时时离目的地多远？

推进农村土地集约式管理，提高土地的使用效率是新农村建设的一项重要举措．某村在小城镇建设中集约了2400亩土地，计划对其进行平整．经投标，由甲乙两个工程队来完成平整任务．甲工程队每天可平整土地45亩，乙工程队每天可平整土地30亩．已知乙工程队每天的工程费比甲工程队少500元，当甲工程队所需工程费为12000元，乙工程队所需工程费为9000元时，两工程队工作天数刚好相同．

（1）甲乙两个工程队每天各需工程费多少元？

（2）现由甲乙两个工程队共同参与土地平整，已知两个工程队工作天数均为正整数，且所有土地刚好平整完，总费用不超过110000元．

①甲乙两工程队分别工作的天数共有多少种可能？

②写出其中费用最少的一种方案，并求出最低费用．

在"新冠"疫情期间，全国人民"众志成城，同心抗疫"，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元 $/$ 件，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量 $y$ （单位：件）与线下售价 $x$ （单位：元 $/$ 件， $12⩽x<24)$ 满足一次函数的关系，部分数据如下表：

$x$ （元     $/$ 件）	12	13	14	15	16
$y$ （件     $)$	1200	1100	1000	900	800

（1）求 $y$ 与 $x$ 的函数关系式；

（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为400件．试问：当 $x$ 为多少时，线上和线下月利润总和达到最大？并求出此时的最大利润．

某班级45名同学自发筹集到1700元资金，用于初中毕业时各项活动的经费．通过商议，决定拿出不少于544元但不超过560元的资金用于请专业人士拍照，其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品．已知每件文化衫28元，每本相册20元．

（1）设用于购买文化衫和相册的总费用为 $W$元，求总费用 $W$（元 $)$与购买的文化衫件数 $t$（件 $)$的函数关系式．

（2）购买文化衫和相册有哪几种方案？为使拍照的资金更充足，应选择哪种方案，并说明理由．

宏兴企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的出厂价为60元．工人甲第 $x$天生产的产品数量为 $y$件， $y$与 $x$满足如下关系： $y=\left\{\begin{array}{c}7.5x(0⩽x⩽4)\\ 5x+10(4<x⩽14)\end{array}\right.$．

（1）工人甲第几天生产的产品数量为70件？

（2）设第 $x$天生产的产品成本为 $P$元 $/$件， $P$与 $x$的函数图象如图．工人甲第 $x$天创造的利润为 $W$元，求 $W$与 $x$的函数关系式，并求出第几天时，利润最大，最大利润是多少？

甲、乙两动点分别从线段 $\mathit{AB}$的两端点同时出发，甲从点 $A$出发，向终点 $B$运动，乙从点 $B$出发，向终点 $A$运动．已知线段 $\mathit{AB}$长为 $90\mathit{cm}$，甲的速度为 $2.5\mathit{cm}/s$．设运动时间为 $x\left(s\right)$，甲、乙两点之间的距离为 $y\left(\mathit{cm}\right)$， $y$与 $x$的函数图象如图所示，则图中线段 $\mathit{DE}$所表示的函数关系式为　　．（并写出自变量取值范围）

如图，在平面直角坐标系中，矩形 $\mathit{ABCD}$的边 $\mathit{AB}$在 $x$轴上， $\mathit{AB}$、 $\mathit{BC}$的长分别是一元二次方程 $x^2-7x+12=0$的两个根 $(\mathit{BC}>\mathit{AB})$， $\mathit{OA}=2\mathit{OB}$，边 $\mathit{CD}$交 $y$轴于点 $E$，动点 $P$以每秒1个单位长度的速度，从点 $E$出发沿折线段 $\mathit{ED}-\mathit{DA}$向点 $A$运动，运动的时间为 $t(0⩽t<6)$秒，设 $\mathit{\Delta BOP}$与矩形 $\mathit{AOED}$重叠部分的面积为 $S$．

（1）求点 $D$的坐标；

（2）求 $S$关于 $t$的函数关系式，并写出自变量的取值范围；

（3）在点 $P$的运动过程中，是否存在点 $P$，使 $\mathit{\Delta BEP}$为等腰三角形？若存在，直接写出点 $P$的坐标；若不存在，请说明理由．

为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买2个甲种文具、1个乙种文具共需花费35元；购买1个甲种文具、3个乙种文具共需花费30元．

（1）求购买一个甲种文具、一个乙种文具各需多少元？

（2）若学校计划购买这两种文具共120个，投入资金不少于955元又不多于1000元，设购买甲种文具 $x$个，求有多少种购买方案？

（3）设学校投入资金 $W$元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？