在▱ABCD中, ,AE平分 交BC于点E,DF平分∠ADC交BC于点F,且 ,则AB的长为( )
A.3B.5C.2或3D.3或5
如图,在四边形 ABCD中,∠ B=∠ C=90°, AB> CD, AD= AB+ CD.
(1)利用尺规作∠ ADC的平分线 DE,交 BC于点 E,连接 AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①证明: AE⊥ DE;
②若 CD=2, AB=4,点 M, N分别是 AE, AB上的动点,求 BM+ MN的最小值.

在▱ ABCD中, AE平分∠ BAD交边 BC于 E, DF平分∠ ADC交边 BC于 F,若 AD=11, EF=5,则 AB= .
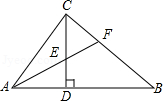
如图,在Rt△ ABC中,∠ ACB=90°, CD⊥ AB,垂足为 D, AF平分∠ CAB,交 CD于点 E,交 CB于点 F.若 AC=3, AB=5,则 CE的长为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知线段  ,分别以
,分别以  、
、  为圆心,大于
AB为半径作弧,连接弧的交点得到直线
为圆心,大于
AB为半径作弧,连接弧的交点得到直线  ,在直线
,在直线  上取一点
上取一点  ,使得
,使得  ,延长
,延长  至
至  ,求
,求  的度数为
的度数为 


| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )

A.150°B.130°C.120°D.100°
(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中, 的三个顶点均在格点上.
①请按要求画图:将 绕点 顺时针方向旋转 ,点 的对应点为点 ,点 的对应点为点 .连接 ;
②在①中所画图形中, .
(2)【问题解决】
如图2,在 中, , ,延长 到 ,使 ,将斜边 绕点 顺时针旋转 到 ,连接 ,求 的度数.
(3)【拓展延伸】
如图3,在四边形 中, ,垂足为 , , , , 为常数),求 的长(用含 的式子表示).

如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.

如图1, 中,点 , , 分别在边 , , 上, ,点 在线段 上, , , .

(1)填空:与 相等的角是 ;
(2)用等式表示线段 与 的数量关系,并证明;
(3)若 , (如图 ,求 的值.
如图, 是 的直径,点 ,点 在 上, , 与 相交于点 , 与 相切于点 ,与 延长线相交于点 .
(1)求证: .
(2)若 , ,求 的半径.

如图,在菱形 中, ,点 , 分别在 , 上,且 , 与 相交于点 , 与 相交于点 .下列结论:① ;② ;③若 ,则 ;④ .其中正确的结论有 .(只填序号即可)

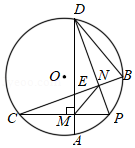
如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)求证: 为 的中点.
(2)若 的半径为8, 的度数为 ,求线段 的长.
初步尝试
(1)如图①,在三角形纸片中,
,将
折叠,使点
与点
重合,折痕为
,则
与
的数量关系为 ;
思考说理
(2)如图②,在三角形纸片中,
,
,将
折叠,使点
与点
重合,折痕为
,求
的值;
拓展延伸
(3)如图③,在三角形纸片中,
,
,
,将
沿过顶点
的直线折叠,使点
落在边
上的点
处,折痕为
.
①求线段的长;
②若点是边
的中点,点
为线段
上的一个动点,将
沿
折叠得到△
,点
的对应点为点
,
与
交于点
,求
的取值范围.

试题篮
()