如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.
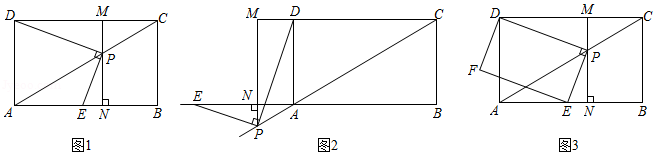
如图,把某矩形纸片 沿 , 折叠(点 、 在 边上,点 , 在 边上),使点 和点 落在 边上同一点 处, 点的对称点为 、 点的对称点为 ,若 , , ,则矩形 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.

如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 , 轴,则 的值为

| A. |
|
B. |
3 |
C. |
4 |
D. |
|
如图,在矩形 中, ,点 是线段 延长线上的一个动点,连接 ,过点 作 交射线 于点 .
(1)如图1,若 ,则 与 之间的数量关系是 ;
(2)如图2,若 ,试判断 与 之间的数量关系,写出结论并证明;(用含 的式子表示)
(3)若 ,连接 交 于点 ,连接 ,当 时,求 的长.

如图,在矩形 中,对角线 的垂直平分线分别与边 和边 的延长线交于点 , ,与边 交于点 ,垂足为点 .
(1)求证: ;
(2)若 , ,请直接写出 的长为 .

如图,在矩形 中, , ,对角线 , 相交于点 ,点 为边 上一动点,连接 ,以 为折痕,将 折叠,点 的对应点为点 ,线段 与 相交于点 .若 为直角三角形,则 的长为 .

如图,在矩形 中, , ,以点 为圆心, 长为半径画弧交边 于点 ,连接 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, , ,点 和点 分别为 , 上的点,将 沿 翻折,使点 落在 上的点 处,过点 作 交 于点 ,过点 作 交 于点 .若四边形 与四边形 的面积相等,则 的长为 .

如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ; ;按照此规律继续进行下去,若矩形 的面积等于2,则△ 的面积为 .(用含正整数 的式子表示)
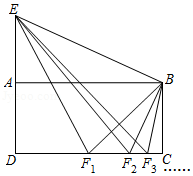
如图,四边形 是矩形,点 是 边上的动点(点 与点 、点 不重合),则 的值为

| A. |
1 |
B. |
|
C. |
2 |
D. |
无法确定 |
如图,在平面直角坐标系中,抛物线 与 轴正半轴交于点 ,且点 的坐标为 ,过点 作垂直于 轴的直线 . 是该抛物线上的任意一点,其横坐标为 ,过点 作 于点 , 是直线 上的一点,其纵坐标为 .以 , 为边作矩形 .
(1)求 的值.
(2)当点 与点 重合时,求 的值.
(3)当矩形 是正方形,且抛物线的顶点在该正方形内部时,求 的值.
(4)当抛物线在矩形 内的部分所对应的函数值 随 的增大而减小时,直接写出 的取值范围.

【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .


试题篮
()