如图,在矩形 中, , ,若点 , 分别在 , 上,且 , , , 分别是 的三等分点,则四边形 的面积为

| A. |
1 |
B. |
|
C. |
2 |
D. |
4 |
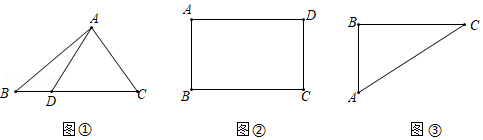
问题提出
(1)如图①,已知直线及
外一点
,试在直线
上确定
、
两点,使
,并画出这个
.
问题探究
(2)如图②,是边长为28的正方形
的对称中心,
是
边上的中点,连接
.试在正方形
的边上确定点
,使线段
和
将正方形
分割成面积之比为
的两部分.求点
到点
的距离.
问题解决
(3)如图③,有一个矩形花园,
,
.根据设计要求,点
、
在对角线
上,且
,并在四边形区域
内种植一种红色花卉,在矩形内其他区域均种植一种黄色花卉.已知种植这种红色花卉每平方米需210元,种植这种黄色花卉每平方米需180元.试求按设计要求,完成这两种花卉的种植至少需费用多少元?(结果保留整数.参考数据:
,

如图,在矩形 中, , ,过矩形的对称中心 的直线 ,分别与 、 交于点 、 ,且 .若 为 的中点,连接 并延长,与 交于点 ,则 的长为

| A. |
8 |
B. |
|
C. |
|
D. |
|
如图,在中,
,
是
的外接圆,点
在
上,且
,过点
作
的垂线,与
的延长线相交于点
,并与
的延长线相交于点
.
(1)求证:是
的切线;
(2)若的半径
,
,求
的长.

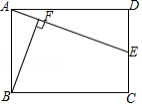
如图,在矩形 中, , .若点 是边 的中点,连接 ,过点 作 交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
问题提出
(1)如图①,已知 ,请画出 关于直线 对称的三角形.
问题探究
(2)如图②,在矩形 中, , , , ,是否在边 、 上分别存在点 、 ,使得四边形 的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材 , 米, 米,现想从此板材中裁出一个面积尽可能大的四边形 部件,使 , 米, ,经研究,只有当点 、 、 分别在边 、 、 上,且 ,并满足点 在矩形 内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形 部件?若能,求出裁得的四边形 部件的面积;若不能,请说明理由.

问题提出
(1)如图①,在 中, , 为 上一点, ,则 面积的最大值是 .
问题探究
(2)如图②,已知矩形 的周长为12,求矩形 面积的最大值.
问题解决
(3)如图③, 是葛叔叔家的菜地示意图,其中 米, 米, 米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形 ,且满足 .你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
已知点,
,
,连接
,
得到矩形
,点
的边
上,将边
沿
折叠,点
的对应点为
.若点
到矩形较长两对边的距离之比为
,则点
的坐标为 .
如图,在矩形中,点
为
的中点,点
为射线
上一动点,△
与
关于
所在直线对称,连接
,分别交
、
于点
、
,
,
.若
与
相似,则
的长为 .

试题篮
()