如图,在四边形 ABCD中,∠ B=60°,∠ D=30°, AB= BC.
(1)求∠ A+∠ C的度数;
(2)连接 BD,探究 AD, BD, CD三者之间的数量关系,并说明理由;
(3)若 AB=1,点 E在四边形 ABCD内部运动,且满足 AE 2= BE 2+ CE 2,求点 E运动路径的长度.

如图,在正方形 ABCD中, AB=6, M是对角线 BD上的一个动点(0< DM< BD),连接 AM,过点 M作 MN⊥ AM交 BC于点 N.
(1)如图①,求证: MA= MN;
(2)如图②,连接 AN, O为 AN的中点, MO的延长线交边 AB于点 P,当 时,求 AN和 PM的长;
(3)如图③,过点 N作 NH⊥ BD于 H,当 AM=2 时,求△ HMN的面积.

爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线, 于点P,像△ABC这样的三角形均为“中垂三角形”.设 .
【特例探究】
(1)如图1,当 , 时,a= ,b= ;
如图2,当 , 时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且 ,连接AF、BE、CE,且 于E,AF与BE相交点G, , ,求AF的长.

如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1) ;(2) ;(3) ;(4)在旋转过程中,当△BEF与△COF的面积之和最大时, ;(5) .

如图,矩形OABC的两边OA,OC分别在x轴和y轴的正半轴上,点B的坐标为( ),点D在CB上,且CD:DB=2:1,OB交AD于点E.平行于x轴的直线l从原点O出发,以每秒1个单位长度的速度沿y轴向上平移,到C点时停止;l与线段OB,AD分别相交与M,N两点,以MN为边作等边△MNP(点P在线段MN的下方).设直线l的运动时间为t(秒),△MNP与△OAB重叠部分的面积为S(平分单位).
(1)直接写出点E的坐标;
(2)求S与t的函数关系式;
(3)是否存在某一时刻t,使得 成立?若存在,请求出此时t的值;若不存在,请说明理由.

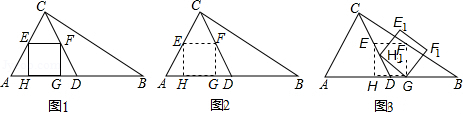
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.
邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第 n次操作余下的四边形是菱形,则称原平行四边形为 n阶准菱形,如图1,▱ ABCD中,若 AB=1, BC=2,则▱ ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是 阶准菱形;已知▱ ABCD的邻边长分别为 a, b( a> b),满足 a=8 b+ r, b=5 r,请写出▱ ABCD是 阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把▱ ABCD沿 BE折叠(点 E在 AD上),使点 A落在 BC边上的点 F处,得到四边形 ABFE.请证明四边形 ABFE是菱形.

如图, M、 N是正方形 ABCD的边 CD上的两个动点,满足 AM= BN,连接 AC交 BN于点 E,连接 DE交 AM于点 F,连接 CF,若正方形的边长为4,则线段 CF的最小值是 .

如图①,正方形 ABCD中,点 O是对角线 AC的中点,点 P是线段 AO上(不与 A, O重合)的一个动点,过点 P作 PE⊥ PB且 PE交边 CD于点 E.
(1)求证: PB= PE.
(2)如图②,若正方形 ABCD的边长为2,过 E作 EF⊥ AC于点 F,在 P点运动的过程中, PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
(3)如图③,用等式表示线段 PC, PA, CE之间的数量关系.

阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.
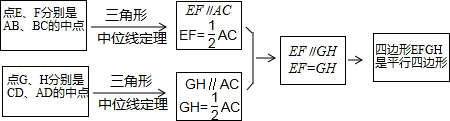
结合小敏的思路作答
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决以下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
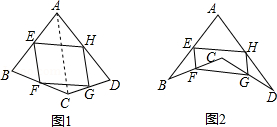
如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(Ⅰ)若△PCD是等腰三角形时,求AP的长;
(Ⅱ)若 ,求CF的长.
现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是 ;
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)

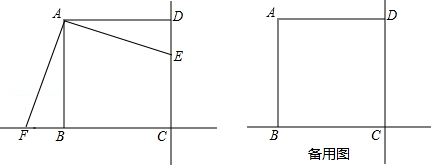
已知正方形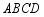 ,点
,点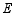 在直线
在直线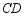 上.
上.
(1)若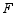 是直线
是直线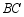 上一点,且
上一点,且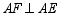 ,求证:
,求证: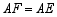 ;(请利用图1所给的图形加以证明)
;(请利用图1所给的图形加以证明)
(2)写出(1)中命题的逆命题,并画出一个图形说明该逆命题是假命题;
(3)若点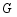 在直线
在直线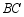 上,且
上,且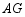 平分
平分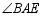 ,探索线段
,探索线段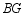 、
、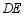 、
、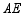 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.

试题篮
()