点 、 为半径是3的圆周上两点,点 为 的中点,以线段 、 为邻边作菱形 ,顶点 恰在该圆直径的三等分点上,则该菱形的边长为
A. 或 B. 或 C. 或 D. 或
如图,已知 的直径 ,弦 , 是 的中点,过点 作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)求 的长.

如图, 是半圆直径,半径 于点 , 为半圆上一点, , 与 交于点 ,连接 、 ,给出以下三个结论:① 平分 ;② ;③ ,其中正确结论的序号是 .

如图, 内接于 , 是 的直径,点 是 上的定点, 平分 交 于点 , ,交 延长线于点 .
(1)求证: 与 相切;
(2)作 于点 , 于点 ,试判断线段 、 、 三者之间的数量关系,并证明你的结论(不用尺规作图的方法补全图形).
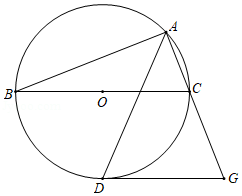
如图, 、 为 的直径,且 ,点 在 上,连接 、 , 于点 ,若 ,则 的度数是

A. B. C. D.
如图,在 中, ,以 为直径的 交 于点 ,且点 是 的中点,连接 交 于点 ,连接 , .
(1)求证: ;
(2)若 , ,求 的长.

如图,点 在以 为直径的 上,点 是 的中点,过点 作 垂直于 ,交 的延长线于点 ,连接 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
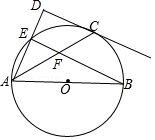
如图,以 的直角边 为直径作 ,交斜边 于点 ,点 为 的中点,连接 并延长交 于点 ,点 恰好落在 的中点,连接 并延长与 的延长线相交于点 ,连接 .
(1)求证: ;
(2)若 ,求 的长.

如图,四边形 内接于 , 是 上一点,且 ,连接 并延长交 的延长线于点 ,连接 .若 , ,则 的度数为
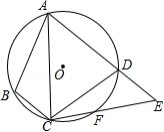
A. B. C. D.
如图, 是 的外接圆, 平分 交 于点 ,交 于点 ,过点 作直线 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 的平分线 交 于点 ,求证: ;
(3)在(2)的条件下,若 , ,求 的长.
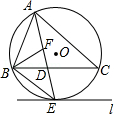
如图, 是 的直径, , 是 上的点,且 , 分别与 , 相交于点 , ,则下列结论:
① ;② ;③ 平分 ;④ ;⑤ ;⑥ ,其中一定成立的是

A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤
如图,四边形 内接于 , , ,垂足为 ,点 在 的延长线上,且 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的值.

如图,四边形 内接于 , , ,垂足为 ,点 在 的延长线上,且 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的值.

试题篮
()