某个长方体主视图是边长为1cm的正方形.沿这个正方形的对角线向垂直于正方形的方向将长方体切开,截面是一个正方形.那么这个长方体的俯视图是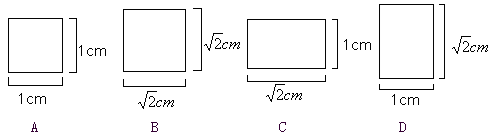
如图,直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D是BC上一点,BD= OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△ ,求△
,求△ 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.
如图,菱形 的对角线 与 相交于点 ,点 、 分别为边 、 的中点,连接 、 、 .求证:四边形 是菱形.
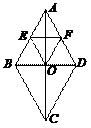
若等腰梯形ABCD的上、下底之和为2,并且两条对角线所成的锐角为60°,则等腰梯形ABCD的面积为 。
如图,在□ ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 。
如图,梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.
求证:四边形ABCD是等腰梯形.
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,
且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.
图①是一个边长为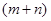 的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )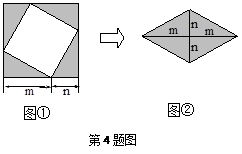
A.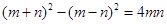 |
B.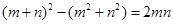 |
C.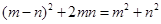 |
D.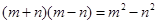 |
在四边形 中,点E,F,G,H分别是边AB,BC,CD,DA的中点,如果四边形EFGH为菱形,那么四边形ABCD是 (只要写出一种即可).
中,点E,F,G,H分别是边AB,BC,CD,DA的中点,如果四边形EFGH为菱形,那么四边形ABCD是 (只要写出一种即可).
数学课上,李老师出示了这样一道题目:如图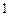 ,正方形
,正方形 的边长为
的边长为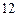 ,
,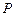 为边
为边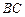 延长线上的一点,
延长线上的一点,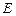 为
为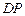 的中点,
的中点,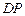 的垂直平分线交边
的垂直平分线交边 于
于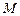 ,交边
,交边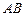 的延长线于
的延长线于 .当
.当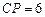 时,
时,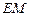 与
与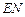 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过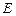 作直线平行于
作直线平行于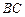 交
交 ,
,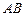 分别于
分别于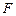 ,
,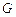 ,如图
,如图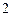 ,则可得:
,则可得: ,因为
,因为 ,所以
,所以 .可求出
.可求出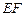 和
和 的值,进而可求得
的值,进而可求得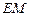 与
与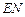 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
如图,是一张宽 的矩形台球桌
的矩形台球桌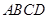 ,一球从点
,一球从点 (点
(点 在长边
在长边 上)
上)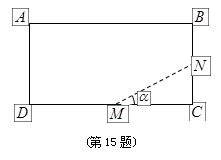
出发沿虚线 射向边
射向边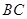 ,然后反弹到边
,然后反弹到边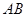 上的
上的 点. 如果
点. 如果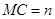 ,
,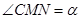 .那么
.那么 点与
点与 点的距离为 .
点的距离为 .
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
如图,在□ABCD中,∠DAB=60°,AB=15㎝.
已知⊙O的半径等于3㎝,AB,AD分别与⊙O相切于点E,F.⊙O在□ABCD内沿AB方向滚动,与BC边相切时运动停止.试求⊙O滚过的路程.
.
从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后,将其截成四个相同的等腰梯形﹙如图①﹚,可以拼成一个平行四边形﹙如图②﹚. 
现有一平行四边形纸片ABCD﹙如图③﹚,已知∠A=45°,AB=6,AD=4.若将该纸片按图②方式截成四个相同的等腰梯形,然后按图①方式拼图,则得到的大正方形的面积为 .
试题篮
()