如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为
| A.2 | B. |
C. |
D. |
不能判断四边形ABCD是平行四边形的是( )
| A.AB=CD,AD=BC | B.AB=CD,AB∥CD |
| C.AB=CD,AD∥BC | D.AB∥CD,AD∥BC |
如图2,梯形ABCD中,AB∥CD,且AB=2CD,E、F分别是AB、BC的中点,EF与BD相交于点M。
⑴求证:△EDM∽△FBM
⑵若DB=9,求BM的长
顺次连结任意四边形四边的中点得到的新四边形一定是
| A.菱形 | B.矩形 | C.正方形 | D.平行四边形 |
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD = 2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为 
本题10分)
(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。
(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
如图9,边长为5的正方形 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)( )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
的坐标;若不存在,说明理由.
某过街天桥的截面图为梯形,如图7所示,其中天桥斜面 的坡度为
的坡度为
( 是指铅直高度
是指铅直高度 与水平宽度
与水平宽度 的比),
的比), 的长为10m,天桥另一斜面
的长为10m,天桥另一斜面
坡角 =
= .
.
(1)写出过街天桥斜面 的坡度;
的坡度;
(2)求 的长;
的长;
(3)若决定对该过街天桥进行改建,使 斜面的坡度变缓,将其
斜面的坡度变缓,将其 坡角改为
坡角改为 ,
,
方便群众,改建后斜面为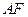 .试计算此改建需占路面的宽度
.试计算此改建需占路面的宽度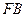 的长(结果精确0.01)
的长(结果精确0.01)
如图5,在平行四边形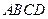 中,
中,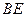 平分
平分 交
交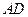 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
.
求证:(1) ;
;
(2)若 ,则判断四边形
,则判断四边形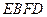 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.
如图3,四边形 为菱形,点
为菱形,点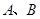 在以点
在以点 为圆心的
为圆心的 上,
上,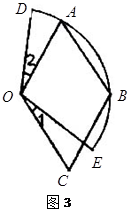
若 则扇形
则扇形 的面积为
的面积为
A. |
B.2 |
C. |
D.3 |
如图11-①, 为
为
 的直径,
的直径, 与
与
 相切于点
相切于点 与
与
 相切于点
相切于点 ,点
,点 为
为 延长线上一点,且
延长线上一点,且

(1)求证: 为
为
 的切线;
的切线;
(2)连接 ,
, 的延长线与
的延长线与 的延长线交于点(如图11-②所示).若
的延长线交于点(如图11-②所示).若 ,求线段
,求线段 和
和 的长.
的长.
正方形 、正方形
、正方形 和正方形
和正方形 的位置如图4所示,点
的位置如图4所示,点 在线段
在线段 上,正方形
上,正方形 的边长为4,则
的边长为4,则 的面积为:
的面积为:
| A.10 | B.12 | C.14 | D.16 |
试题篮
()