如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当 时,对应的函数值
时,对应的函数值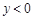 ;
;
③当 时,函数值y随x的增大而增大.
时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是: (写出一个即可)
试题篮
()