如图，已知点F的坐标为（3，0），点A，B分别是某函数图象与x轴、y轴的交点，P是此图象上的一动点．设P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5﹣
（0≤x≤5），给出以下四个结论：
①AF=2；②BF=5；③OA=5；④OB=4
其中正确结论的序号是 ．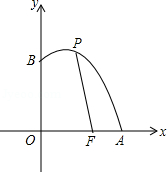
如图，在平面直角坐标系中，将一块腰长为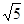
的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，顶点A的坐标为
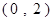，点B在抛物线
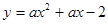上．
（1）直角顶点C的坐标为 ；
（2）求抛物线的解析式；
（3）若点D是（1）中所求抛物线在第三象限内的一个动点，连接BD、CD．当△BCD的面积最大时，求点D的坐标．
定义一种变换：平移抛物线F1得到抛物线F2，使F2经过F1的顶点A．设F2的对称轴分别交F1，F2于点D，B，点C是点A关于直线BD的对称点．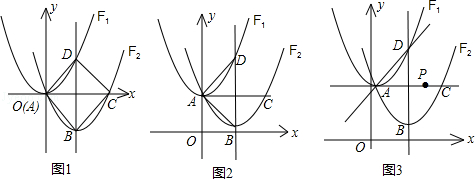
（1）如图1，若F1：y=x2，经过变换后，得到F2：y=x2+bx，点C的坐标为（2，0），则：
①b的值等于 ；
②四边形ABCD为（ ）
A、平行四边形；B、矩形；C、菱形；D、正方形．
（2）如图2，若F1：y=ax2+c，经过变换后，点B的坐标为（2，c﹣1），求△ABD的面积；
（3）如图3，若F1：y=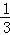
x2﹣
x+
，经过变换后，AC=2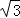
，点P是直线AC上的动点，求点P到点D的距离和到直线AD的距离之和的最小值．
如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．
（1）求该抛物线的解析式及顶点M坐标；
（2）求△BCM面积与△ABC面积的比；
（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．
抛物线y=﹣x2+（m﹣1）x+m与y轴交于点（0，3）．
（1）求抛物线的解析式；
（2）求抛物线与坐标轴的交点坐标；
（3）①当x取什么值时，y＞0？②当x取什么值时，y的值随x的增大而减小？
如图，直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的个数是（ ）
①abc＞0；②3a+b＞0；③﹣1＜k＜0；④k＞a+b；⑤ac+k＞0．
A．1 B．2 C．3 D．4
抛物线y=﹣x2+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是（ ）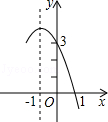
| A．﹣4＜x＜1 | B．﹣3＜x＜1 | C．x＜﹣4或x＞1 | D．x＜﹣3或x＞1 |
如图，AC=BC，点D是以线段AB为弦的圆弧的中点，AB=4，点E、F分别是线段CD，AB上的动点．设AF=x，AE2﹣FE2=y，则能表示y与x的函数关系的图象是（ ）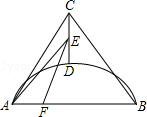
A． |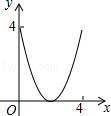
B． |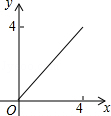
C． |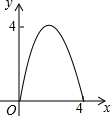
D． |
已知抛物线y=ax2+2x+c与x轴交于A（1，0）和点B，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式．
（2）如图1，已知点H的坐标为（0，1），设点M为y轴左侧抛物线上的一个动点，试猜想：是否存在这样的点M，使|MA﹣MH|的值最大，如果存在，请求出点M的坐标；如果不存在，请说明理由．
（3）如图2，过x轴上点E（﹣2，0）作ED⊥AB交抛物线于点D，在y轴上找一点F，使△EDF的周长最小，求出此时点F的坐标；
（4）如图3，已知点N（0，﹣1）．问在抛物线上是否存在点Q（点Q在y轴的左侧），使得△QNC的面积与△QNA的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．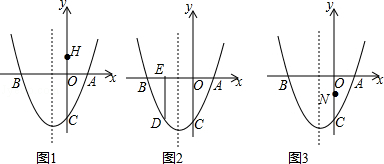
已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为A（﹣1，0），另一交点为B，与y轴的交点坐标为C（0，3）．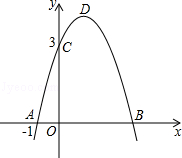
（1）求出b，c的值，并写出此二次函数的解析式；
（2）求出顶点D的坐标以及S△BCD面积；
（3）根据图象，写出函数值y为正数时，自变量x的取值范围．
试题篮
()
粤公网安备 44130202000953号
的顶点坐标是 ．
