初中数学三角形的五心试题

下列说法：①一条直角边和斜边上的高对应相等的两个直角三角形全等；②有两条边相等的两个直角三角形全等；③若两个直角三角形面积相等，则它们全等；④两边和其中一边的对角对应相等的两个三角形全等．其中错误的个数是（　　）

A．1

B．2

C．3

D．4

等腰三角形的一边长为5，一边为11，则它的周长为(     )

A．21

B．27

C．21或27

D．16

如图，梯形ABCD中，AD∥BC，AB = BC = DC，点E、F分别在AD、AB上，且.

(1)求证：；
(2)连结AC，若，求的度数.

如图，一辆汽车在一个十字路口遇到红灯刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA＝30°和∠DCB＝60°，如果斑马线的宽度是AB＝3米，驾驶员与车头的距离是0.8米，这时汽车车头与斑马线的距离x是多少?

如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，求折痕CE的长．

如图，在□ABCD中，EF∥BD，分别交BC、CD于点P、Q，分别交AB、AD 的延长线于点E、F，BE=BP．

（1）若∠E=70度，求∠F的度数．
（2）求证：△ABD是等腰三角形．

两直角边长分别为6和8的直角三角形的斜边上的中线长为      .

如图，△ABC是边长为5的等边三角形，将△ABC绕点C顺时针旋转120°，得到△EDC,连接BD，交AC于F.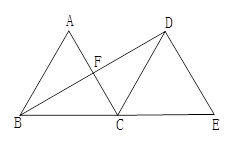

（1）猜想AC与BD的位置关系，并证明你的结论；
（2）求线段BD的长.

已知一等腰三角形的两边长x、y满足方程组则此等腰三角形的周长为        ．

如图，∠A+∠ABC+∠C+∠D+∠E+∠F＝_____．

如图，已知AB∥CF，E是DF的中点，若AB=9cm，CF=6cm，则BD=__________cm．

如图AD⊥BD，AE平分∠BAC，∠ACD=70°，∠B=30°．则∠DAE的度数为_____________°．

如图，△ABC是面积为a的等边三角形，AD是BC边上的高，点E、F是AD上
的两点．则图中阴影部分的面积为___________．

如图，若∠DBC=∠D，BD平分∠ABC，∠ABC=50°，则∠BCD的大小为（    ）

A．50°

B．100°

C．130°

D．150°

如图，在△ABC中，AD⊥BC于D，AE平分∠BAC．


（1）若∠C－∠B＝30°，则∠DAE＝________．
（2）若∠C－∠B＝（∠C＞∠B），求∠DAE的度数（用含的代数式表示）．