如图BC是半圆⊙O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD 交于点E。求证: , P是BD的中点,过P作PQ∥AB交OA于点Q,若AE=3,CD=
, P是BD的中点,过P作PQ∥AB交OA于点Q,若AE=3,CD= ,求PQ的长。
,求PQ的长。
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=4cm,则CB的长为
A. |
B. |
C. |
D.4 |
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0, ),直线l2的函数表达式为
),直线l2的函数表达式为 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.求直线l1的函数表达式;
当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=
 时a的值.
时a的值.当⊙C和直线l2不相离时,已知⊙C的
 半径R=
半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A ′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是 .
如图4,在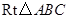 中,
中,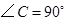 ,
,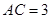 .将其绕
.将其绕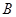 点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.该圆环的面积为
点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.该圆环的面积为 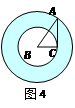
A.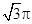 |
B. |
C. |
D. |
试题篮
()